题目内容
已知向量
=(2cos(
+x),-1),
=(-sin(
-x),cos2x),定义函数f(x)=
•
.
(1)求函数f(x)的表达式,并指出其最大值和最小值;
(2)在锐角△ABC中,角A,B,C的对边分别为a,b,c,且f(A)=1,bc=8,求△ABC的面积S.
| OP |
| π |
| 2 |
| OQ |
| π |
| 2 |
| OP |
| OQ |
(1)求函数f(x)的表达式,并指出其最大值和最小值;
(2)在锐角△ABC中,角A,B,C的对边分别为a,b,c,且f(A)=1,bc=8,求△ABC的面积S.
(1)∵
=(2cos(
+x),-1)=(-2sinx,-1),
=(-sin(
-x),cos2x)=(-cosx,cos2x).
∴f(x)=
•
=(-2sinx,-1)•(-cosx,cos2x)
=(-2sinx,-1)•(-cosx,cos2x)
=(-sinx)•(-cosx)-cos2x
=sin2x-cos2x
=
sin(2x-
),
∴f(x)的最大值和最小值分别是
和-
.
(2)∵f(A)=1,
∴
sin(2x-
)=1,
∴sin(2A-
)=
.
又∵0<A<π
∴2A-
=
或2A-
=
.
∴A=
或A=
.
又∵△ABC为锐角三角形,
∴A=
.
∵bc=8,
∴△ABC的面积S═
×8×
=2
.
| OP |
| π |
| 2 |
| OQ |
| π |
| 2 |
∴f(x)=
| OP |
| OQ |
=(-2sinx,-1)•(-cosx,cos2x)
=(-2sinx,-1)•(-cosx,cos2x)
=(-sinx)•(-cosx)-cos2x
=sin2x-cos2x
=
| 2 |
| π |
| 4 |
∴f(x)的最大值和最小值分别是
| 2 |
| 2 |
(2)∵f(A)=1,
∴
| 2 |
| π |
| 4 |
∴sin(2A-
| π |
| 4 |
| ||
| 2 |
又∵0<A<π
∴2A-
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
∴A=
| π |
| 4 |
| π |
| 2 |
又∵△ABC为锐角三角形,
∴A=
| π |
| 4 |
∵bc=8,
∴△ABC的面积S═
| 1 |
| 2 |
| ||
| 2 |
| 2 |

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
 ,并写出函数
,并写出函数 的最小正周期;
的最小正周期;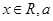 为非零常数,且
为非零常数,且 ,试问
,试问 是周期函数吗?证明你的结论.
是周期函数吗?证明你的结论. 其中
其中
 在
在 中,
中, 分别是角的对边,且
分别是角的对边,且 .
. ,
, ,求
,求 ,若
,若 ,则
,则 ( )
( )
