题目内容
如图,∠BAC=90°,在平面α内,PA是α的斜线,∠PAB=∠PAC=60°.求PA与平面α所成的角.
解析:作PO⊥平面α于O,作OM⊥AC于M,ON⊥AB于N,连结PM、PN,

则PM⊥AC,PN⊥AB.在Rt△PMA和Rt△PNA中,∠PAM=∠PAN=60°.
∴△PMA≌△PNA.∴PM=PN.
∵OM、ON分别是PM、PN在平面α内的射影,
∴OM=ON.于是AO是∠BAC的平分线.设PA=a,∠PAM=60°,
∴AM=![]() ,∠OAM=45°.
,∠OAM=45°.
∴AO=![]() a.
a.
在△POA中,cos∠PAO=![]() ,
,
∴∠PAO=45°,
即PA与平面α所成的角为45°.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,已知四面体P-ABC中,PA=PB=PC,且AB=AC,∠BAC=90°,则异面直线PA与BC所成的角为
如图,已知四面体P-ABC中,PA=PB=PC,且AB=AC,∠BAC=90°,则异面直线PA与BC所成的角为 如图∠BAC=90°,等腰直角三角形ABC所在的平面与正方形ABDE所在 的平面互相垂直,则异面直线AD与BC所成角的大小是
如图∠BAC=90°,等腰直角三角形ABC所在的平面与正方形ABDE所在 的平面互相垂直,则异面直线AD与BC所成角的大小是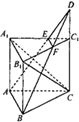 (2013•成都二模)如图,在直三棱柱(侧棱与底面垂直的三棱柱)ABC-A1B1C1中,AC=AA1=2AB=2,∠BAC=90°,点D是侧棱CC1 延长线上一点,EF是平面ABD与平面A1B1C1的交线.
(2013•成都二模)如图,在直三棱柱(侧棱与底面垂直的三棱柱)ABC-A1B1C1中,AC=AA1=2AB=2,∠BAC=90°,点D是侧棱CC1 延长线上一点,EF是平面ABD与平面A1B1C1的交线.