题目内容
已知函数f(x)=m•2x+2•3x,m∈R.
(1)当m=-9时,求满足f(x+1)>f(x)的实数x的范围;
(2)若 对任意的x∈R恒成立,求实数m的范围;
对任意的x∈R恒成立,求实数m的范围;
(3)若存在m使f(x)≤ax对任意的x∈R恒成立,其中a为大于1的正整数,求a的最小值.
解:(1)当m=-9时,f(x)=-9•2x+2•3x,
∵f(x+1)>f(x)
∴-9•2x+1+2•3x+1>-9•2x+2•3x,
即4•3x>9•2x,即
∴x>2;
(2)∵ 对任意的x∈R恒成立,
对任意的x∈R恒成立,
∴m•2x+2•3x 对任意的x∈R恒成立,
对任意的x∈R恒成立,
不等式两边同时除以2x得 ≥2×
≥2×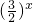 +m
+m
令t=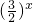 >0,则t2-2t-m≥0即m≤t2-2t=(t-1)2-1对于任意正实数t恒成立
>0,则t2-2t-m≥0即m≤t2-2t=(t-1)2-1对于任意正实数t恒成立
∴m≤-1;
(3)由(2)知,存在m∈(-∞,-1]使f(x)≤( )x对任意的x∈R恒成立,
)x对任意的x∈R恒成立,
欲使f(x)≤ax对任意的x∈R恒成立,只需a≥ ,
,
∵a∈N+,∴a的最小值为5.
分析:(1)将m=-9代入解析式,然后化简不等式f(x+1)>f(x),最后利用指数函数的单调性即可求出所求;
(2)将m参变量分离,然后利用换元法转化成求二次函数的最值,从而可求出m的取值范围;
(3)由(2)知,存在m∈(-∞,-1]使f(x)≤( )x对任意的x∈R恒成立,欲使f(x)≤ax对任意的x∈R恒成立,只需a≥
)x对任意的x∈R恒成立,欲使f(x)≤ax对任意的x∈R恒成立,只需a≥ ,从而可求出a的最小值.
,从而可求出a的最小值.
点评:本题主要考查了函数恒成立问题,以及指数函数的综合应用,同时考查了转化的思想和运算求解的能力,属于中档题.
∵f(x+1)>f(x)
∴-9•2x+1+2•3x+1>-9•2x+2•3x,
即4•3x>9•2x,即

∴x>2;
(2)∵
 对任意的x∈R恒成立,
对任意的x∈R恒成立,∴m•2x+2•3x
 对任意的x∈R恒成立,
对任意的x∈R恒成立,不等式两边同时除以2x得
 ≥2×
≥2×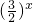 +m
+m令t=
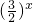 >0,则t2-2t-m≥0即m≤t2-2t=(t-1)2-1对于任意正实数t恒成立
>0,则t2-2t-m≥0即m≤t2-2t=(t-1)2-1对于任意正实数t恒成立∴m≤-1;
(3)由(2)知,存在m∈(-∞,-1]使f(x)≤(
 )x对任意的x∈R恒成立,
)x对任意的x∈R恒成立,欲使f(x)≤ax对任意的x∈R恒成立,只需a≥
 ,
,∵a∈N+,∴a的最小值为5.
分析:(1)将m=-9代入解析式,然后化简不等式f(x+1)>f(x),最后利用指数函数的单调性即可求出所求;
(2)将m参变量分离,然后利用换元法转化成求二次函数的最值,从而可求出m的取值范围;
(3)由(2)知,存在m∈(-∞,-1]使f(x)≤(
 )x对任意的x∈R恒成立,欲使f(x)≤ax对任意的x∈R恒成立,只需a≥
)x对任意的x∈R恒成立,欲使f(x)≤ax对任意的x∈R恒成立,只需a≥ ,从而可求出a的最小值.
,从而可求出a的最小值.点评:本题主要考查了函数恒成立问题,以及指数函数的综合应用,同时考查了转化的思想和运算求解的能力,属于中档题.

练习册系列答案
相关题目