题目内容
已知函数![]() ,其中
,其中![]() 是自然对数的底数,
是自然对数的底数,![]() .
.
(1)当![]() 时,解不等式
时,解不等式![]() ;
;
(2)当![]() 时,求整数的所有值,使方程
时,求整数的所有值,使方程![]() 在
在![]() 上有解;
上有解;
(3)若![]() 在
在![]() 上是单调增函数,求
上是单调增函数,求![]() 的取值范围.
的取值范围.
解:(1)因为![]() ,所以不等式
,所以不等式![]() 即为
即为![]() ,又因为
,又因为![]() ,所以不等式可化为
,所以不等式可化为![]() ,所以不等式
,所以不等式![]() 的解集为
的解集为![]() . (4 分)
. (4 分)
(2)当![]() 时, 方程即为
时, 方程即为![]() ,由于
,由于![]() ,所以
,所以![]() 不是方程的解,所以原方程等价于
不是方程的解,所以原方程等价于![]() ,令
,令![]() ,因为
,因为![]() 对于
对于![]() 恒成立,
恒成立,
所以![]() 在
在![]() 和
和![]() 内是单调增函数, 又
内是单调增函数, 又![]() ,
,![]() ,
,![]() ,
,![]() ,所以方程
,所以方程![]() 有且只有两个实数根,且分别在区间
有且只有两个实数根,且分别在区间![]() 和
和![]() 上,所以整数的所有值为
上,所以整数的所有值为![]() . (8分)
. (8分)


练习册系列答案
相关题目
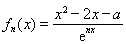
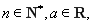
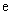
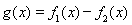


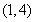

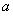
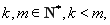
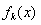
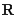
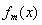






 ,其中
,其中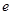 是自然对数的底数,
是自然对数的底数,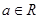 .
.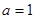 ,求曲线
,求曲线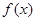 在点
在点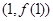 处的切线方程;
处的切线方程;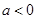 ,求
,求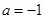 ,函数
,函数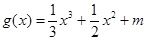 的图象有3个不同的交点,求实数
的图象有3个不同的交点,求实数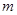 的取值范围.
的取值范围. 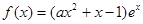 ,其中
,其中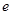 是自然对数的底数,
是自然对数的底数,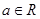 .
.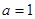 ,求曲线
,求曲线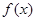 在点
在点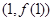 处的切线方程;
处的切线方程;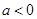 ,求
,求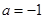 ,函数
,函数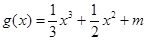 的图象有3个不同的交点,求实数
的图象有3个不同的交点,求实数 的取值范围.
的取值范围.