题目内容
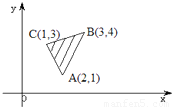
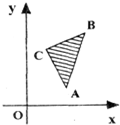 已知x,y的可行域如图阴影部分,其中A(2,1),B(3,4),C(1,3),z=mx+y(m>0)在该区域内取得最小值的最优解有无数个,则m=
已知x,y的可行域如图阴影部分,其中A(2,1),B(3,4),C(1,3),z=mx+y(m>0)在该区域内取得最小值的最优解有无数个,则m=2
2
.分析:由z=mx+y(m>0)得y=-mx+z(m>0),根据条件要使z=mx+y(m>0)在该区域内取得最小值的最优解有无数个,则直线y=-mx+z(m>0)的斜率-m=kAC,利用斜率公式进行求解即可.
解答:解:由z=mx+y(m>0)得y=-mx+z(m>0),
则直线y=-mx+z(m>0)的斜率为-m<0,
要使z=mx+y(m>0)在该区域内取得最小值的最优解有无数个,
则直线y=-mx+z(m>0)的斜率-m=kAC,
∵A(2,1),C(1,3),
∴kAC=
=
=-2,
即-m=-2,
解得m=2.
故答案为:2.
则直线y=-mx+z(m>0)的斜率为-m<0,
要使z=mx+y(m>0)在该区域内取得最小值的最优解有无数个,
则直线y=-mx+z(m>0)的斜率-m=kAC,
∵A(2,1),C(1,3),
∴kAC=
| 3-1 |
| 1-2 |
| 2 |
| -1 |
即-m=-2,
解得m=2.
故答案为:2.
点评:本题主要考查线性规划的应用,利用z=mx+y(m>0)在该区域内取得最小值的最优解有无数个,得到直线y=-mx+z(m>0)的斜率-m=kAC是解决本题的关键.

练习册系列答案
相关题目
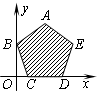 已知以x,y为自变量的目标函数z=kx+y (k>0)的可行域如图阴影部分(含边界),且A(1,2),B(0,1),C(
已知以x,y为自变量的目标函数z=kx+y (k>0)的可行域如图阴影部分(含边界),且A(1,2),B(0,1),C( 已知x,y的可行域如图阴影部分,z=mx+y(m>0),在该区域内取得最小值的最优解有无数个,则m=( )
已知x,y的可行域如图阴影部分,z=mx+y(m>0),在该区域内取得最小值的最优解有无数个,则m=( ) 已知x,y的可行域如图阴影部分,z=mx+y(m>0),在该区域内取得最小值的最优解有无数个,则m=
已知x,y的可行域如图阴影部分,z=mx+y(m>0),在该区域内取得最小值的最优解有无数个,则m=