题目内容
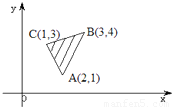
 已知x,y的可行域如图阴影部分,z=mx+y(m>0),在该区域内取得最小值的最优解有无数个,则m=( )
已知x,y的可行域如图阴影部分,z=mx+y(m>0),在该区域内取得最小值的最优解有无数个,则m=( )分析:由题设条件,目标函数z=mx+y(m>0)取得最小值的最优解有无数个,知取得最优解必在边界上而不是在顶点上,目标函数中两个系数皆为正,故最大值应在左上方边界AC上取到,即mx+y=0应与直线AC平行;进而计算可得答案.
解答:解:由题意,目标函数z=mx+y(m>0)取得最小值的最优解有无数个,
知取得最优解必在边界上而不是在顶点上,目标函数中两个系数皆为正,
最优解应在线段AC上取到,故mx+y=0应与直线AC平行
∵kAB=
=-2,
∴-m=-2,
∴m=2,
故选C.
知取得最优解必在边界上而不是在顶点上,目标函数中两个系数皆为正,
最优解应在线段AC上取到,故mx+y=0应与直线AC平行

∵kAB=
| 3-1 |
| 1-2 |
∴-m=-2,
∴m=2,
故选C.
点评:本题考查线性规划最优解的判定,属于该知识的逆用题型,知最优解的特征,判断出最优解的位置求参数.

练习册系列答案
相关题目
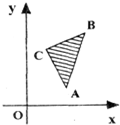 已知x,y的可行域如图阴影部分,其中A(2,1),B(3,4),C(1,3),z=mx+y(m>0)在该区域内取得最小值的最优解有无数个,则m=
已知x,y的可行域如图阴影部分,其中A(2,1),B(3,4),C(1,3),z=mx+y(m>0)在该区域内取得最小值的最优解有无数个,则m=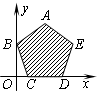 已知以x,y为自变量的目标函数z=kx+y (k>0)的可行域如图阴影部分(含边界),且A(1,2),B(0,1),C(
已知以x,y为自变量的目标函数z=kx+y (k>0)的可行域如图阴影部分(含边界),且A(1,2),B(0,1),C( 已知x,y的可行域如图阴影部分,z=mx+y(m>0),在该区域内取得最小值的最优解有无数个,则m=
已知x,y的可行域如图阴影部分,z=mx+y(m>0),在该区域内取得最小值的最优解有无数个,则m=