题目内容

椭圆C1：
x2
a2
+
y2
b2
=1（a＞b＞0）的左准线为l，左、右焦点分别为F1，F2，抛物线C2的准线也为l，焦点为F2，记C1与C2的一个交点为P，则
|F1F2|
|PF1|
-
|PF1|
|PF2|
=（　　）
A、
1
2
B、1
C、2
D、与a，b的取值无关
分析：P到椭圆的左准线的距离设为d，先利用椭圆的第二定义求得|PF1|=
c
a
d，利用抛物线的定义可知|PF2|=d，最后根据椭圆的定义可知|PF2|+|PF1|=2a且
|PF1|
|PF2|
=
c
a
，求得|PF2|，|PF1|，可得
|F1F2|
|PF1|
-
|PF1|
|PF2|
．
解答：解：椭圆的离心率为
c
a
，
P到椭圆的左准线的距离设为d，
则|PF1|=
1
2
d，|PF2|+|PF1|=2a，又|PF2|=d，
∴d=|PF2|=
2a2
a+c
，|PF1|=
2ac
a+c
．
得
|F1F2|
|PF1|
-
|PF1|
|PF2|
=
2c
2ac
a+c
-
c
a
=1．
故选B．
点评：本题主要考查了椭圆的简单性质．解题的关键是灵活利用椭圆和抛物线的定义．本题考查圆锥曲线的综合应用，解题时要认真审题，注意公式的合理运用．
练习册系列答案
相关题目
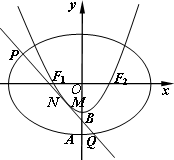精英家教网设椭圆C1：
x2
a2
+
y2
b2
=1(a＞b＞0)的左、右焦点分别是F1、F2，下顶点为A，线段OA的中点为B（O为坐标原点），如图．若抛物线C2：y=x2-1与y轴的交点为B，且经过F1，F2点．
（Ⅰ）求椭圆C1的方程；
（Ⅱ）设M（0，-
4
5
），N为抛物线C2上的一动点，过点N作抛物线C2的切线交椭圆C1于P、Q两点，求△MPQ面积的最大值．
已知椭圆C1：
x2
a2
+
y2
b2
=1(a＞b＞0)的右焦点F2与抛物线C2：y2=4x的焦点重合，椭圆C1与抛物线C2在第一象限的交点为P，|PF2|=
5
3
，求椭圆C1的方程．
（2013•三门峡模拟）已知椭圆C1：
x2
a2
+
y2
b2
=1（a＞b＞0）的长轴长为4，离心率为
1
2
，F1、F2分别为其左右焦点．一动圆过点F2，且与直线x=-1相切．
（Ⅰ）（ⅰ）求椭圆C1的方程； （ⅱ）求动圆圆心C轨迹的方程；
（Ⅱ）在曲线上C有两点M、N，椭圆C1上有两点P、Q，满足MF2与
NF2
共线，
PF2
与
QF2
共线，且
PF2
•
MF2
=0，求四边形PMQN面积的最小值．
已知椭圆C1：
x2
A2
+
y2
B2
=1(A＞B＞0)和双曲线C2：
x2
a2
-
y2
b2
=1(a＞0，b＞0)有相同的焦点F1、F2，2c是它们的共同焦距，且它们的离心率互为倒数，P是它们在第一象限的交点，当cos∠F1PF2=60°时，下列结论中正确的是（　　）
（2013•汕头一模）已知椭圆C1：
x2
a2
+
y2
b2
=1(a＞b＞0)的左、右焦点分别为F1、F2，右顶点为A，离心率e=
1
2

（1）设抛物线C2：y2=4x的准线与x轴交于F1，求椭圆的方程；
（2）设已知双曲线C3以椭圆C1的焦点为顶点，顶点为焦点，b是双曲线C3在第一象限上任意-点，问是否存在常数λ（λ＞0），使∠BAF1=λ∠BF1A恒成立？若存在，求出λ的值；若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网