题目内容
将直线 绕着其与
绕着其与 轴的交点逆时针旋转
轴的交点逆时针旋转 得到直线m,则m与圆
得到直线m,则m与圆 截得弦长为( )
截得弦长为( )
A. | B. | C. | D. |
D
解析试题分析:l上点M的坐标为(2,0),l的倾斜角 的正切tan
的正切tan =2。
=2。
逆时针旋转45°后,新的直线倾斜角 =
= +45°。
+45°。
则k=tan =tan(
=tan( +45°)=-3,所以直线md 方程为y=-3(x-2),即3x+y-6=0。
+45°)=-3,所以直线md 方程为y=-3(x-2),即3x+y-6=0。
(0,0)到直线m距离为 =
= ,所以由圆的弦长公式得m与圆
,所以由圆的弦长公式得m与圆 截得弦长为
截得弦长为 ,故选D。
,故选D。
考点:本题主要考查在直线的旋转,直线和圆的位置关系。
点评:小综合题,本题较全面的考查了直线的旋转,直线的倾斜角和斜率之间的关系,以及直线和圆的位置关系。圆中的“特征三角形”应予足够关注。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若直线 与圆
与圆 有公共点,则实数
有公共点,则实数 取值范围是( )
取值范围是( )
A. | B. |
C. | D. |
若方程 表示一个圆,则有( )
表示一个圆,则有( )
A. | B.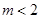 | C. | D. |
若直线 (
( )被圆
)被圆 截得的弦长为4,则
截得的弦长为4,则 的最小值为( )
的最小值为( )
A. | B. | C.2 | D.4 |
以两点 和
和 为直径端点的圆的方程是
为直径端点的圆的方程是
A. | B. |
C. | D. |
圆C:x2+y2+2x+4y-3=0上到直线 :x+y+1=0的距离为
:x+y+1=0的距离为 的点共有( )
的点共有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
已知圆C与圆(x-1)2+y2=1关于直线y=-x对称,则圆C的方程( )
| A.(x+1)2+y2=1 | B.x2+y2=1 |
| C.x2+(y+1)2=1 | D.x2+(y-1)2=1 |
由直线 上的一点向圆
上的一点向圆 引切线,则切线长的最小值为( )
引切线,则切线长的最小值为( )
| A.1 | B. | C.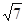 | D.3 |
 与圆
与圆 有公共点
有公共点 则斜率
则斜率 的取值范围是( )
的取值范围是( )






