题目内容
规定[x]表示不超过x的最大整数,f(x)= ,若方程f(x)=ax+1有且仅有四个实数根,则实数a的取值范围是( )
,若方程f(x)=ax+1有且仅有四个实数根,则实数a的取值范围是( )
A. | B. | C. | D. |
B
解析试题分析:当x∈[0,+∞)时,f(x)是以1为周期的函数,且f(x)=x-k,x∈[k,k+1)(k∈N),
当x∈(-∞,0)时,f(x)是指数型函数,而y=ax+1为过定点(0,1)斜率为a的直线,
在同一个坐标系中作出它们的图象为:
由图象可知,当直线介于两红色线之间时,符合题意,而它们的斜率分别为?
故实数a的取值范围为[? ],故选B.
],故选B.
考点:根的存在性及个数的判断

练习册系列答案
相关题目
若函数 满足
满足 ,且
,且 ,则
,则 的值为( )
的值为( )
A. | B. | C. | D. |
已知数列{an}的通项为 ,我们把使乘积
,我们把使乘积 为整数的n叫做“优数”,则在
为整数的n叫做“优数”,则在 内最大的“优数”为( ).
内最大的“优数”为( ).
| A.510 | B.512 | C.1022 | D.1024 |
在下列区间中,函数 的零点所在的区间为( )
的零点所在的区间为( )
A.(- ,0) ,0) | B.(0, ) ) | C.( , , ) ) | D.( , , ) ) |
若函数 在
在 上单调递减,则
上单调递减,则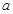 的取值范围是
的取值范围是
A. | B. | C. | D. |
 在
在 上是减函数,则
上是减函数,则 的取值范围是( )
的取值范围是( )
A.[ | B.[  ] ] | C.(  | D.(  ] ] |
若函数 的图象不经过第二象限,则有
的图象不经过第二象限,则有
A. | B. | C. | D. |
下列四类函数中,具有性质“对任意的 ,
, ,函数
,函数 满足
满足 ”
”
的是( )
| A.幂函数 | B.对数函数 | C.指数函数 | D.余弦函数 |
图中曲线是幂函数y=xn在第一象限的图象,已知n取±3,± 四个值,则相应于曲线C1,C2,C3,C4的n依次为 ( )
四个值,则相应于曲线C1,C2,C3,C4的n依次为 ( )
A.-3,- , , ,3 ,3 | B.3, ,- ,- ,-3 ,-3 |
C.- ,-3,3, ,-3,3, | D.3, ,-3,- ,-3,- |