题目内容
【题目】已知函数![]() .
.
(1)求函数![]() 的定义域;
的定义域;
(2)判断函数![]() 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(3)若函数![]() ,求函数
,求函数![]() 的零点.
的零点.
【答案】(1) ![]() (2)
(2) ![]() 为奇函数(3)
为奇函数(3)![]()
【解析】试题分析:(1)要使函数![]() 有意义,
有意义, ![]() 必须满足
必须满足![]() ,从而得到定义域;(2)利用奇偶性定义判断奇偶性;(3)函数
,从而得到定义域;(2)利用奇偶性定义判断奇偶性;(3)函数![]() 的零点即方程
的零点即方程![]() 的根.即
的根.即![]() 的根,又
的根,又![]() 为奇函数,所以
为奇函数,所以![]() .易证:
.易证: ![]() 在定义域
在定义域![]() 上为增函数,∴由
上为增函数,∴由![]() 得
得![]() ,从而解得函数
,从而解得函数![]() 的零点.
的零点.
试题解析:
(1)要使函数![]() 有意义,
有意义, ![]() 必须满足
必须满足![]() ,∴
,∴![]() ,
,
因此, ![]() 的定义域为
的定义域为![]() .
.
(2)函数![]() 为奇函数.
为奇函数.
∵![]() 的定义域为
的定义域为![]() ,对
,对![]() 内的任意
内的任意![]() 有:
有:
![]()
![]() ,
,
所以, ![]() 为奇函数.
为奇函数.
(3)函数![]() 的零点即方程
的零点即方程![]() 的根.即
的根.即![]() 的根,
的根,
又![]() 为奇函数,所以
为奇函数,所以![]() .
.
任取![]() ,且
,且![]() ,
,
![]()
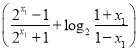
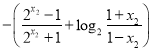

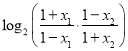
∵![]() ,∴
,∴![]() ,∴
,∴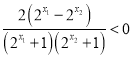
∵![]() 且
且![]() ,∴
,∴![]()
![]() ,
,
∴![]() ,∴
,∴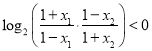 ,
,
∴![]() ,即
,即![]() ,∴
,∴![]() 在定义域
在定义域![]() 上为增函数,
上为增函数,
∴由![]() 得
得![]() 解得
解得![]() 或
或![]() ,
,
验证当![]() 时,
时, ![]() 不符合题意,当
不符合题意,当![]() 时,符合题意,
时,符合题意,
所以函数![]() 的零点为
的零点为![]() .
.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
【题目】某公司为了研究年宣传费![]() (单位:千元)对销售量
(单位:千元)对销售量![]() (单位:吨)和年利润
(单位:吨)和年利润![]() (单位:千元)的影响,搜集了近 8 年的年宣传费
(单位:千元)的影响,搜集了近 8 年的年宣传费![]() 和年销售量
和年销售量![]() 数据:
数据:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 38 | 40 | 44 | 46 | 48 | 50 | 52 | 56 |
| 45 | 55 | 61 | 63 | 65 | 66 | 67 | 68 |
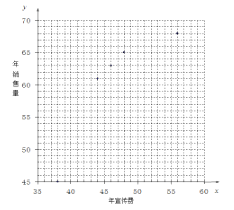
(Ⅰ)请补齐表格中 8 组数据的散点图,并判断![]() 与
与![]() 中哪一个更适宜作为年销售量
中哪一个更适宜作为年销售量![]() 关于年宣传费
关于年宣传费![]() 的函数表达式?(给出判断即可,不必说明理由)
的函数表达式?(给出判断即可,不必说明理由)
(Ⅱ)若(Ⅰ)中的![]() ,且产品的年利润
,且产品的年利润![]() 与
与![]() ,
, ![]() 的关系为
的关系为![]() ,为使年利润值最大,投入的年宣传费 x 应为何值?
,为使年利润值最大,投入的年宣传费 x 应为何值?
