题目内容
函数数列{fn(x)}满足:f1(x)=
(x>0),fn+1(x)=f1[fn(x)]
(1)求f2(x),f3(x);
(2)猜想fn(x)的表达式,并证明你的结论.
| x | ||
|
(1)求f2(x),f3(x);
(2)猜想fn(x)的表达式,并证明你的结论.
(1)f2(x)=f1(f1(x))=
=
f3(x)=f1(f2(x))=
=
(2)猜想:fn(x)=
(n∈N*)
下面用数学归纳法证明:
①当n=1时,f1(x)=
2,已知,显然成立
②假设当n=K(K∈N*)4时,猜想成立,即fk(x)=
则当n=K+1时,fk+1(x)=f1(fk(x))=
=
=
即对n=K+1时,猜想也成立.
结合①②可知:猜想fn(x)=
对一切n∈N*都成立.
| f1(x) | ||||
|
| x | ||
|
| f2(x) | ||||
|
| x | ||
|
(2)猜想:fn(x)=
| x | ||
|
下面用数学归纳法证明:
①当n=1时,f1(x)=
| x | ||
|
②假设当n=K(K∈N*)4时,猜想成立,即fk(x)=
| x | ||
|
则当n=K+1时,fk+1(x)=f1(fk(x))=
| fk(x) | ||||
|
| ||||||
|
| x | ||
|
即对n=K+1时,猜想也成立.
结合①②可知:猜想fn(x)=
| x | ||
|

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
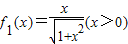 ,fn+1(x)=f1[fn(x)]
,fn+1(x)=f1[fn(x)]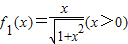 ,fn+1(x)=f1[fn(x)]
,fn+1(x)=f1[fn(x)]