题目内容
如图是函数 的导函数
的导函数 的图象,给出下列命题
的图象,给出下列命题
① 是函数
是函数 的极值点.
的极值点.
② 是函数
是函数 的极小值点.
的极小值点.
③ 在
在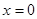 处切线斜率大于
处切线斜率大于 .
.
④ 在区间
在区间 上单调递减.则正确命题的序号是 .
上单调递减.则正确命题的序号是 .
①③④
解析试题分析:根据原函数和导函数的关系,本题中导函数的图像可知: 在
在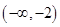 单调递减;
单调递减; 单调递增;当
单调递增;当 时取得极小值,无极大值,当
时取得极小值,无极大值,当 时,
时, ,
, 在
在 处切线斜率大于
处切线斜率大于 ,综上正确命题的序号是:①③④.
,综上正确命题的序号是:①③④.
考点:1.原函数和导函数的关系;2.函数的单调性,极值.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
已知 ,则
,则 ( )
( )
A.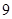 | B. | C. | D. |
已知函数 的导函数
的导函数 的图象如图所示,
的图象如图所示, ,令
,令 ,则不等式
,则不等式 的解集是( )
的解集是( )
A. | B. |
C. | D.[-1,2] |
已知定义在R上的奇函f(x)的导函数为f’(x),当x<0时,f(x)满足 ,则f(x)在R上的零点个数为( )
,则f(x)在R上的零点个数为( )
| A.1 | B.3 | C.5 | D.1或3 |
同时具有性质“⑴ 最小正周期是 ;⑵ 图象关于直线
;⑵ 图象关于直线 对称;⑶ 在
对称;⑶ 在 上是减函数”的一个函数可以是
上是减函数”的一个函数可以是
A. | B. | C. | D. |
若 ,
, ,
, ,则
,则
A. | B. | C. | D. |
在 中,
中, ,
, ,
,  在边
在边 上,且
上,且 ,则
,则 ( )
( )
A. | B. | C. | D. |
 ,则
,则
 = .
= .