题目内容
已知定义在R上的奇函f(x)的导函数为f’(x),当x<0时,f(x)满足 ,则f(x)在R上的零点个数为( )
,则f(x)在R上的零点个数为( )
| A.1 | B.3 | C.5 | D.1或3 |
A
解析试题分析:∵当x<0时,f(x)满足 ,∴当x<0时,f(x)满足
,∴当x<0时,f(x)满足 ,令
,令 ,∴
,∴ ,所以
,所以 ,所以
,所以 在(-∞,0)上单调递增,所以
在(-∞,0)上单调递增,所以 ,即
,即 ;当x>0时,则-x<0,所以
;当x>0时,则-x<0,所以 ,所以
,所以 ,所以
,所以 ,所以
,所以 ,所以
,所以 在(0,+∞)上单调递增,所以
在(0,+∞)上单调递增,所以 ,所以当x∈(0,+∞)时,f(x)>0;又因为f(0)=0;综上f(x)只有一个零点.
,所以当x∈(0,+∞)时,f(x)>0;又因为f(0)=0;综上f(x)只有一个零点.
考点:函数的零点.

练习册系列答案
相关题目
已知 ,
, ,
, ,则a,b,c的大小关系是
,则a,b,c的大小关系是
| A.a > b > c | B.c > b > a | C.c > a >b | D.a>c>b |
要得到函数 的图象,只需将函数
的图象,只需将函数 的图象
的图象
A.向右平移 个单位长度 个单位长度 |
B.向左平移 个单位长度 个单位长度 |
C.向右平移 个单位长度 个单位长度 |
D.向左平移 个单位长度 个单位长度 |
已知 ,
, ,
, ( )
( )
A. | B. | C. | D. |
 上的函数
上的函数 同时满足以下三个条件:①
同时满足以下三个条件:①  ;
;  ;③当
;③当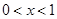 时,
时, ,则
,则 .
. ;
; 在定义域内可导,
在定义域内可导, 的图象如图,则导函数
的图象如图,则导函数 的图象可能为 ( )
的图象可能为 ( )

 的导函数
的导函数 的图象,给出下列命题
的图象,给出下列命题
 是函数
是函数 是函数
是函数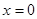 处切线斜率大于
处切线斜率大于 .
. 上单调递减.则正确命题的序号是 .
上单调递减.则正确命题的序号是 . 是曲线y="ln" x(x>0)的一条切线,则实数b=
是曲线y="ln" x(x>0)的一条切线,则实数b=