题目内容
P是菱形ABCD所在平面外一点,∠ABC=60°,PA=AC=a,PB=PD=
a,求证:PA⊥平面ABCD.
证明:∵底面ABCD是菱形,∠ABC=60°,
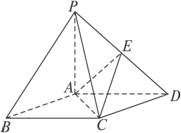
∴AB=AD=AC=a.
在△PAB中,由PA2+AB2=
知PA⊥AB.
同理,PA⊥AD.又AB∩AD=A,
∴PA⊥平面ABCD.
练习册系列答案
举一反三单元同步过关卷系列答案
相关题目
a,求证:PA⊥平面ABCD.举一反三单元同步过关卷系列答案题目内容
P是菱形ABCD所在平面外一点,∠ABC=60°,PA=AC=a,PB=PD=a,求证:PA⊥平面ABCD.
证明:∵底面ABCD是菱形,∠ABC=60°,
∴AB=AD=AC=a.
在△PAB中,由PA2+AB2=
知PA⊥AB.
同理,PA⊥AD.又AB∩AD=A,
∴PA⊥平面ABCD.
举一反三单元同步过关卷系列答案
已知P是菱形ABCD所在平面外一点，且PB=PD，求证：平面PAC⊥平面PBD．
