题目内容
在正三棱柱ABC-A1B1C1中,AB=3,高为2,则它的外接球上A、B两点的球面距离为
2π-2arccos
| 1 |
| 8 |
2π-2arccos
.| 1 |
| 8 |
分析:由已知中三棱柱的底面边长及高,求出棱柱底面外接圆的半径及球心距,进而求出三棱柱外接球的球半径,求出球心角,利用弧长公式,即可求得结论.
解答:解:∵正三棱柱的底面边长AB=3,∴底面所在平面截其外接球所成的圆O′的半径r=
∵正三棱柱的高为2cm,∴球心到圆O′的球心距d=1
根据球心距,截面圆半径,球半径构成直角三角形,满足勾股定理,我们易得球半径R满足:R2=r2+d2=4
∴R=2
∴cos∠AOB=
=-
∴∠AOB=π-arccos
∴外接球上A、B两点的球面距离为2(π-arccos
)=2π-2arccos
故答案为:2π-2arccos
.
| 3 |
∵正三棱柱的高为2cm,∴球心到圆O′的球心距d=1
根据球心距,截面圆半径,球半径构成直角三角形,满足勾股定理,我们易得球半径R满足:R2=r2+d2=4
∴R=2
∴cos∠AOB=
| 22+22-32 |
| 2×2×2 |
| 1 |
| 8 |
∴∠AOB=π-arccos
| 1 |
| 8 |
∴外接球上A、B两点的球面距离为2(π-arccos
| 1 |
| 8 |
| 1 |
| 8 |
故答案为:2π-2arccos
| 1 |
| 8 |
点评:本题考查的知识点是棱柱的几何特征及球面距离,根据已知求出已知三棱柱的外接球半径是解答本题的关键,属于中档题.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
 如图,在正三棱柱ABC-A1B1C1中,AA1=AB,D是AC的中点.
如图,在正三棱柱ABC-A1B1C1中,AA1=AB,D是AC的中点.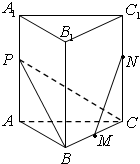 如图,在正三棱柱ABC-A1B1C1中,所有棱的长度都是1,M是BC边的中点,P是AA1边上的点,且
如图,在正三棱柱ABC-A1B1C1中,所有棱的长度都是1,M是BC边的中点,P是AA1边上的点,且 如图,在正三棱柱ABC-A'B'C'中,AB=2,若二面角C'-AB-C的大小为60°,则点C到平面ABC'的距离为
如图,在正三棱柱ABC-A'B'C'中,AB=2,若二面角C'-AB-C的大小为60°,则点C到平面ABC'的距离为