Question

（2011•江西模拟）若函数y=f（x）在其图象上两个不同点处的切线重合，则称这条切线为自公切线，下列函数存在自公切线的序号为

②④

①y=ln|x+1|；②y=x²-|x|；③y=

x2-1

；  ④y=xcosx．

Answer 1

分析：通过画出函数图象，观察其图象是否满足在其上图象上是否存在两个不同点处的切线重合，从而确定是否存在自公切线，从而得到结论．

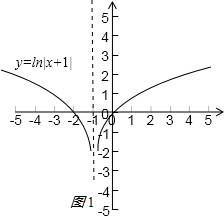
解答：解：函数y=ln|x+1|的图象如图1，显然A不存在；
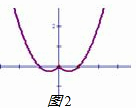
函数 y=x²-|x|的图象如图2显然满足要求，故B存在；
y=

x2-1

即x²-y² =1（y≥0）为等轴双曲线的一部分，不存在自公切线，故C不存在； 
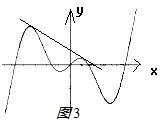
函数 y=xcosx的图象如图3显然满足要求，存在自公切线，故D存在；
 故答案为②④

点评：本题主要考查了利用导数研究曲线上某点切线方程，以及新定义自公切线，题目比较新颖，解题的关键是理解新的定义，同时考查了数形结合的思想，属于中档题．