题目内容

17．在各项均为正值的等比数列{an}中，已知a5、a13分别是方程2x2-mx+2e4=0的两根，则a7a9a11的值为（　　）
A．e6B．$\sqrt{{e}^{5}}$C．e7D．e5

分析 利用根与系数的关系，由已知条件能求出a5•a13=e4，由此利用等比数列的性质能求出a9，即可得出结论．

解答 解：等比数列{an}中，
∵a5、a13分别是方程2x2-mx+2e4=0的两根，
∴a5•a13=e4，
∴a9=e2，
∴a7a9a11=a93=e6，
故选：A．

点评 本题主要考查等比数列的定义和性质，一元二次方程根与系数的关系，属于中档题．

练习册系列答案
相关题目
7．分别写出下列函数：y=log2x，x∈[$\frac{1}{2}$，4]，y=cosx，x∈[-$\frac{π}{3}$，$\frac{π}{2}$]的最小值和最大值．
8．如图，在平面直角坐标系xOy中，一单位圆圆心的初始位置在（0，1），此时圆上点P的位置在（0，0），圆在x轴上沿正向滚动，当圆滚动到圆心位于（a，1）时，则$\overrightarrow{OP}$的坐标为（a-sina，1-cosa）．
5．已知直线（2+λ）x-（1-2λ）y-（6+3λ）=0所经过的定点F恰好是椭圆C的一个焦点，且椭圆C上点到点F的最小距离为2．
（Ⅰ）求椭圆C的标准方程；
（Ⅱ）已知圆O：x2+y2=1，直线l：mx+ny=1，试证明：当点P（m，n）在椭圆C上运动时，直线l与圆C恒相交，并求直线l被圆O所截得的弦长的取值范围．
12．已知△ABC的面积为1，tanB=$\frac{1}{2}$，tanC=-2，求△ABC外接圆的面积以及△ABC的各边长．
2．定义[x]为不超过x的最大整数，如[3.3]=3，[-1.8]=-2，设f（x）=x-[x]，x∈R，要使得方程f（x）=ax恰有2015个实数解，则实数a的取值范围是（　　）
A．（-$\frac{1}{2014}$，-$\frac{1}{2015}$]∪[$\frac{1}{2015}$，$\frac{1}{2014}$）B．（-$\frac{1}{2014}$，-$\frac{1}{2015}$）∪（$\frac{1}{2015}$，$\frac{1}{2014}$）
C．（-$\frac{1}{2013}$，-$\frac{1}{2014}$]∪[$\frac{1}{2016}$，$\frac{1}{2015}$）D．（-$\frac{1}{2014}$，-$\frac{1}{2015}$]∪[$\frac{1}{2016}$，$\frac{1}{2015}$）
9．α=-1，则α的终边所在的象限是（　　）
A．第一象限B．第二象限C．第三象限D．第四象限
3．已知f（x）=$\left\{\begin{array}{l}{x+k（1{-a}^{2}），x≥0}\\{{x}^{2}-4x{+（3-a）}^{2}，x＜0}\end{array}\right.$，a∈R，对任意非零实数x1，存在唯一的非零实数x2（x1≠x2），使得f（x1）=f（x2）成立，则实数k的取值范围是（-∞，0]∪[8，+∞）．
4．如图所示的程序框图，其作用是输入x的值，输出相应的y值，若输入$x=\frac{π}{2}$，则输出的y值为（　　）
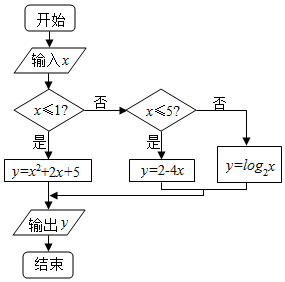
A．2B．${log_2}\frac{π}{2}$C．2-2πD．8

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网