题目内容
6.设函数y=f(x)的定义域为A,集合B={y|y=f(x),x∈A},若B⊆A,则称函数f(x)为定义域A内的“任性函数”.(1)若函数f(x)=m+$\frac{3+{x}^{2}}{x-1}$是定义域A=(2,+∞)内的“任性函数”,则实数m的取值范围是(-4,+∞);(2)已知-2≤a≤2且a≠0,-1≤b≤1,则函数f(x)=ax2+b是定义域A=[0,1]内的“任性函数”的概率为$\frac{1}{8}$.分析 (1)根据“任性函数”的定义,只要函数f(x)=m+$\frac{3+{x}^{2}}{x-1}$是值域B是定义域A=(2,+∞)的子集即可;
(2)由题意,本题是几何概型,只要求出a,b满足的区域面积,利用面积比求概率.
解答 解:(1)由题意函数f(x)=m+$\frac{3+{x}^{2}}{x-1}$是定义域A=(2,+∞),函数f(x)=m+$\frac{3+{x}^{2}}{x-1}$=m+2+(x-1)+$\frac{4}{x-1}$>6+m,
因为f(x)为任性函数,所以6+m≥2,所以m≥-4,故实数m的取值范围是[-4,+∞);
(2)-2≤a≤2且a≠0,-1≤b≤1,对应区域面积为8,
而函数f(x)=ax2+b是定义域A=[0,1]内的“任性函数”的a,b范围是0≤b,a+b≤1或者b≤1,a+b≥0,对应区域面积为$\frac{1}{2}+\frac{1}{2}$=1,如图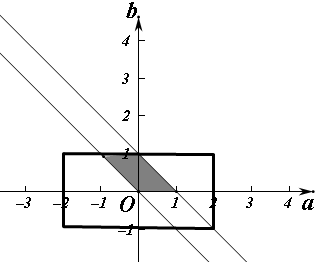
由几何概型的公式得到f(x)为任性函数的概率为$\frac{1}{8}$;
故答案为:[-4,+∞);$\frac{1}{8}$.
点评 本题考查了任性函数的新定义问题和几何概型的概率求法;解答本题的关键是由新定义求出变量范围.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
8.已知集合A={x|x2=1},B={x|ax=1},若B⊆A,则a的取值组成的集合为( )
| A. | Φ | B. | {0} | C. | {-1,0,1} | D. | {-1,1} |
11.已知An2=132,则n=( )
| A. | 11 | B. | 12 | C. | 13 | D. | 14 |
16.已知全集I={-1,-2,-3,0,1},M={-1,0,a2+1},则∁IM为( )
| A. | {-1,-2,-3,1} | B. | {-1,0,1} | C. | {-1,-3} | D. | {-2,-3} |