题目内容
已知函数
(1)求函数f(x)的单调区间;
(2)利用1)的结论求解不等式2|lnx|≤ •|x-1|.并利用不等式结论比较ln2(1+x)与
•|x-1|.并利用不等式结论比较ln2(1+x)与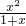 的大小.
的大小.
(3)若不等式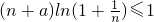 对任意n∈N*都成立,求a的最大值.
对任意n∈N*都成立,求a的最大值.
解:(1) ,定义域x|x>0
,定义域x|x>0

∴f(x)在(0,+∞)上是减函数.
(2)对
当x≥1时,原不等式变为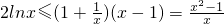
由(1)结论,x≥1时,f(x)≤f(1)=0, 即
即 成立
成立
当0<x≤1时,原不等式变为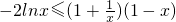 ,即
,即
由(1)结论0<x≤1时,f(x)≥f(1)=0,
综上得,所求不等式的解集是{x|x>0}
∵x>0时, ,即
,即 ,
,
∴
用 (其中x>-1)代入上式中的x,可得
(其中x>-1)代入上式中的x,可得
(3)结论:a的最大值为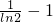
∵n∈N*,∴ ∵
∵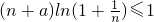 ,∴
,∴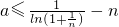
取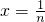 ,则x∈(0,1],∴
,则x∈(0,1],∴
设 ,
,
∵g(x)递减,
∴x=1时
∴a的最大值为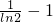 .
.
分析:先求函数的定义域
(1)对函数求导,利用导数在区间(0,+∞)的符号判断函数的单调性.
(2)根据题目中式子的结构,结合(1)中单调性的结论可考虑讨论①x≥1,f(x)≤f(1)=0②0<x<1,f(x)>f(1)=0两种情况对原不等式进行求解.
(3)若不等式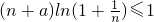 对任意n∈N*都成立?a≤
对任意n∈N*都成立?a≤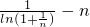 恒成立构造函数g(x)=
恒成立构造函数g(x)=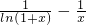 ,利用导数判断该函数的单调性,从而求解函数的最小值,即可求解a的值
,利用导数判断该函数的单调性,从而求解函数的最小值,即可求解a的值
点评:本题主要考查了利用导数判断对数函数的单调性,利用单调性解对数不等式,函数的恒成立问题的求解,综合考查了函数的知识的运用,要求考生具备综合解决问题的能力.
 ,定义域x|x>0
,定义域x|x>0
∴f(x)在(0,+∞)上是减函数.
(2)对

当x≥1时,原不等式变为
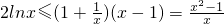
由(1)结论,x≥1时,f(x)≤f(1)=0,
 即
即 成立
成立当0<x≤1时,原不等式变为
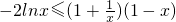 ,即
,即
由(1)结论0<x≤1时,f(x)≥f(1)=0,
综上得,所求不等式的解集是{x|x>0}
∵x>0时,
 ,即
,即 ,
,∴

用
 (其中x>-1)代入上式中的x,可得
(其中x>-1)代入上式中的x,可得
(3)结论:a的最大值为
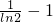
∵n∈N*,∴
 ∵
∵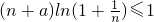 ,∴
,∴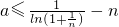
取
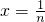 ,则x∈(0,1],∴
,则x∈(0,1],∴
设
 ,
,
∵g(x)递减,
∴x=1时

∴a的最大值为
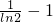 .
.分析:先求函数的定义域
(1)对函数求导,利用导数在区间(0,+∞)的符号判断函数的单调性.
(2)根据题目中式子的结构,结合(1)中单调性的结论可考虑讨论①x≥1,f(x)≤f(1)=0②0<x<1,f(x)>f(1)=0两种情况对原不等式进行求解.
(3)若不等式
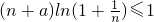 对任意n∈N*都成立?a≤
对任意n∈N*都成立?a≤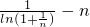 恒成立构造函数g(x)=
恒成立构造函数g(x)=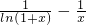 ,利用导数判断该函数的单调性,从而求解函数的最小值,即可求解a的值
,利用导数判断该函数的单调性,从而求解函数的最小值,即可求解a的值点评:本题主要考查了利用导数判断对数函数的单调性,利用单调性解对数不等式,函数的恒成立问题的求解,综合考查了函数的知识的运用,要求考生具备综合解决问题的能力.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目



 的极值点;
的极值点; 过点(0,—1),并且与曲线
过点(0,—1),并且与曲线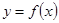 相切,求直线
相切,求直线 ,其中
,其中 ,求函数
,求函数 在
在 上的最小值.(其中e为自然对数的底数)
上的最小值.(其中e为自然对数的底数)