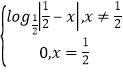Question

【题目】已知F是抛物线y2=4x的焦点，点A，B在该抛物线上且位于x轴的两侧，OA⊥OB（其中O为坐标原点），则△AOB与△AOF面积之和的最小值是（　　）
A.16
B.8
C.8
D.18

Answer 1

【答案】C
【解析】解：设直线AB的方程为：x=ty+m，
点A（x1 ， y1），B（x2 ， y2），直线AB与x轴的交点为M（m，0），
x=ty+m代入y2=4x，可得y2﹣4ty﹣4m=0，
根据韦达定理有y1y2=﹣4m，
∵OA⊥OB，
∴=0，
∴x1x2+y1y2=0，从而（y1y2）2+y1y2=0，
∵点A，B位于x轴的两侧，
∴y1y2=﹣16，故m=4．
不妨令点A在x轴上方，则y1＞0，
又F（1，0），
∴S△ABO+S△AFO=×4×（y1﹣y2）+×y1=y1+
≥8 ，
当且仅当y1= ， 即y1=时，取“=”号，
∴△ABO与△AFO面积之和的最小值是8 ，
故选：C．