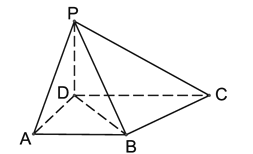
题目内容
【题目】己知函数![]() ,
, ![]() .
.
(I)求函数![]() 上零点的个数;
上零点的个数;
(II)设![]() ,若函数
,若函数![]() 在
在![]() 上是增函数.
上是增函数.
求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)零点个数为![]() (II)
(II)![]() 的取值范围是
的取值范围是![]()
【解析】试题分析:(1)先求得![]() ,
, ![]() 时,
时, ![]() 恒成立,可证明
恒成立,可证明![]() 时,
时, ![]() ,可得
,可得![]() 在
在![]() 上单调递减,根据零点定理可得结果;(2)化简
上单调递减,根据零点定理可得结果;(2)化简![]() 为分段函数
为分段函数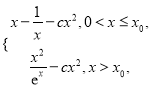 ,利用导数研究函数的单调性,讨论两种情况,分别分离参数求最值即可求得实数
,利用导数研究函数的单调性,讨论两种情况,分别分离参数求最值即可求得实数![]() 的取值范围.
的取值范围.
试题解析:(Ⅰ)函数![]()
![]() ,
,
求导,得![]() ,
,
当![]() 时,
时, ![]() 恒成立,
恒成立,
当![]() 时,
时,  ,
,
∴![]()
![]() ,
,
∴![]() 在
在![]() 上恒成立,故
上恒成立,故![]() 在
在![]() 上单调递减.
上单调递减.
又![]() ,
, ![]() ,
,
曲线![]() 在[1,2]上连续不间断,
在[1,2]上连续不间断,
∴由函数的零点存在性定理及其单调性知,唯一的![]() ∈(1,2),使
∈(1,2),使![]() ,
,
所以,函数![]() 在
在![]() 上零点的个数为1.
上零点的个数为1.
(II)由(Ⅰ)知:当![]() 时,
时, ![]() >0,当
>0,当![]() 时,
时, ![]() <0.
<0.
∴当![]() 时,
时, ![]() =
=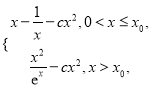
求导,得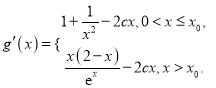
由于函数![]() 在
在![]() 上是增函数, 故
上是增函数, 故![]() 在
在![]() ,
, ![]() 上恒成立.
上恒成立.
①当![]() 时,
时, ![]() ≥0在
≥0在![]() 上恒成立,
上恒成立,
即![]() 在
在![]() 上恒成立,
上恒成立,
记![]() ,
, ![]() ,则
,则![]() ,,
,,
所以, ![]() 在
在![]() 上单调递减,
上单调递减,![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() min=
min= ![]() 极小值=
极小值= ![]()
![]() ,
,
故“![]() 在
在![]() 上恒成立”,只需
上恒成立”,只需![]()
![]() ,即
,即![]() .
.
②当![]() 时,
时, ![]()
![]() ,
,
当![]() 时,
时, ![]() 在
在![]() 上恒成立,
上恒成立,
综合①②知,当![]() 时,函数
时,函数![]() 在
在![]() 上是增函数.
上是增函数.
故实数![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目