题目内容
过点(1,0)的直线l与中心在原点,焦点在x轴上且离心率为
解:由e=![]() =
=![]() 得
得![]() ,从而a2=2b2,c=b.
,从而a2=2b2,c=b.
设椭圆C的方程为x2+2y2=2b2,l的方程为y=k(x-1),代入C方程,得(1+2k2)x2-4k2x+ 2k2-2b2=0,
则x1+x2=![]() ,y1+y2=k(x1-1)+k(x2-1)=k(x1+x2)-2k=-
,y1+y2=k(x1-1)+k(x2-1)=k(x1+x2)-2k=-![]() .
.
直线y=![]() x过AB的中点(
x过AB的中点(![]() ,
,![]() ),则
),则![]() =
=![]() ·
·![]() ,解得k=0或k=-1.
,解得k=0或k=-1.
若k=0,则l:y=0,焦点F(c,0)关于l的对称点就是F点本身,不能在椭圆C上,所以k=0舍去;若k=-1,l:y=-(x-1),即y=-x+1,右焦点为(b,0),其关于l的对称点设为(x′,y′).
则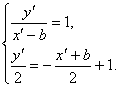 解得
解得![]()
点(1,1-b)在椭圆上,得1+2(1-b)2=2b2,?b2=![]() ,a2=
,a2=![]() .?
.?
∴所求椭圆C的方程为:![]() =1,l的方程为y′=-x+1.
=1,l的方程为y′=-x+1.

练习册系列答案
相关题目
已知抛物线M:y2=4x,圆N:(x-1)2+y2=r2(其中r为常数,r>0).过点(1,0)的直线l交圆N于C、D两点,交抛物线M于A、B两点,且满足|AC|=|BD|的直线l只有三条的必要条件是( )
| A、r∈(0,1] | ||
| B、r∈(1,2] | ||
C、r∈(
| ||
D、r∈[
|
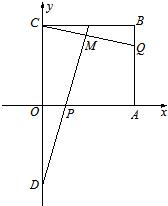 如图所示,在直角坐标平面上的矩形OABC中,|OA|=2,
如图所示,在直角坐标平面上的矩形OABC中,|OA|=2,