Question

据市场调查，某种商品一年内每件出厂价在7千元的基础上，按月呈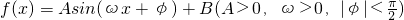的模型波动（x为月份，1≤x≤12，x∈N^*），已知3月份达到最高价9千元，7月份价格最低为5千元，根据以上条件可确定f（x）的解析式为

1. A.
   
2. B.
   
3. C.
   
4. D.
   

Answer 1

A
分析：根据题意，可得当x=3时，函数有最大值为9；当x=7时，函数有最小值5，再利用正弦函数的最值，联列方程组，解之可得A=2，B=7．根据函数的周期T=，结合题意得到ω=，最后用函数取最大值时对应x的值，可得φ=，从而可以确定f（x）的解析式．
解答：∵3月份达到最高价9千元，7月份价格最低为5千元，
∴当x=3时，函数有最大值为9；当x=7时，函数有最小值5
∴，可得
又∵函数的周期T=2（7-3）=8，
∴由T=，得ω==，
∵当x=3时，函数有最大值，
∴3ω+φ=，即+φ=，
结合，取k=0，得φ=
∴f（x）的解析式为：
故选A
点评：本题根据一个实际问题的研究，着重考查了由y=Asin（ωx+φ）的部分图象确定其解析式的知识点，考查了数学应用能力，属于中档题．