题目内容
已知(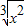 +3x2)n展开式中各项的系数和比各项的二项式系数和大992.求展开式中系数最大的项.
+3x2)n展开式中各项的系数和比各项的二项式系数和大992.求展开式中系数最大的项.
【答案】分析:由题意可得4n-2n=992,求得n=5,设第r+1项的系数最大,则有 ,解得
,解得  ≤r≤
≤r≤ .再由 r∈N,可得r的值.
.再由 r∈N,可得r的值.
解答:解:令x=1可得各项系数和为4n,二项式系数和为2n,
由题意可得4n-2n=992,即(2n-32)(2n+31)=0,
解得2n=32 2n=-31 (舍去),解得n=5.
设第r+1项的系数最大,则有 ,解得
,解得  ≤r≤
≤r≤ .
.
再由 r∈N,可得r=4.
故系数最大的项为 T5= •
• •(3x2)4=405
•(3x2)4=405 .
.
点评:本题主要考查二项式定理的应用,二项式展开式的通项公式,二项式系数的性质,属于中档题.
 ,解得
,解得  ≤r≤
≤r≤ .再由 r∈N,可得r的值.
.再由 r∈N,可得r的值.解答:解:令x=1可得各项系数和为4n,二项式系数和为2n,
由题意可得4n-2n=992,即(2n-32)(2n+31)=0,
解得2n=32 2n=-31 (舍去),解得n=5.
设第r+1项的系数最大,则有
 ,解得
,解得  ≤r≤
≤r≤ .
.再由 r∈N,可得r=4.
故系数最大的项为 T5=
 •
• •(3x2)4=405
•(3x2)4=405 .
.点评:本题主要考查二项式定理的应用,二项式展开式的通项公式,二项式系数的性质,属于中档题.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
 +3x2)n(n∈N)的展开式中,名项系数的和与其各项二项式系数和的比值为32.
+3x2)n(n∈N)的展开式中,名项系数的和与其各项二项式系数和的比值为32.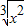 +3x2)n(n∈N)的展开式中,名项系数的和与其各项二项式系数和的比值为32.
+3x2)n(n∈N)的展开式中,名项系数的和与其各项二项式系数和的比值为32.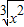 +3x2)n(n∈N)的展开式中,名项系数的和与其各项二项式系数和的比值为32.
+3x2)n(n∈N)的展开式中,名项系数的和与其各项二项式系数和的比值为32.