题目内容
椭圆 的离心率e=
的离心率e= ,过右焦点F的直线l与椭圆C相交于A、B两点,当直线l的斜率为1时,坐标原点O到直线l的距离为
,过右焦点F的直线l与椭圆C相交于A、B两点,当直线l的斜率为1时,坐标原点O到直线l的距离为 .
.
(1)求椭圆C的方程;
(2)如图,椭圆C上是否存在点P,使得当直线l绕点F转到某一位置时,有 成立?若存在,求出所有满足条件的点P的坐标及对应的直线方程;若不存在,请说明理由.
成立?若存在,求出所有满足条件的点P的坐标及对应的直线方程;若不存在,请说明理由.
解:(1)∵O到直线l的距离为 ,l:y=x-c,
,l:y=x-c,
∴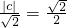 ,∴c=1.
,∴c=1.
∵e= ,∴
,∴ ,∴b2=1.
,∴b2=1.
∴椭圆C的方程为 .
.
(2)设A(x1,y1),B(x2,y2),P(x0,y0)设y=k(x-1)(k≠0)
由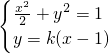 ,消去y得(1+2k2)x2-4k2x+2k2-2=0.
,消去y得(1+2k2)x2-4k2x+2k2-2=0.
∴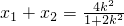 ,
,
∴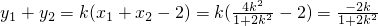 .
.
∵ ,
,
∴x0=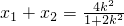 ,
,
∴y0=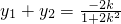 .
.
将P点坐标代入椭圆得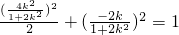 ,
,
∴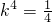 ,∴
,∴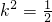 ,
,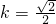 .
.
当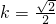 时,
时,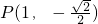 ,直线
,直线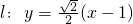 ,
,
当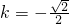 时,
时,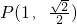 ,直线
,直线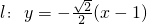 .
.
分析:(1)由O到直线l的距离为 ,l:y=x-c,知
,l:y=x-c,知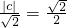 ,c=1.由e=
,c=1.由e= ,知
,知 ,b2=1.由此能求出椭圆C的方程.
,b2=1.由此能求出椭圆C的方程.
(2)设A(x1,y1),B(x2,y2),P(x0,y0)设y=k(x-1)(k≠0)由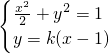 ,得(1+2k2)x2-4k2x+2k2-2=0.由此能求出求出所有满足条件的点P的坐标及对应的直线方程.
,得(1+2k2)x2-4k2x+2k2-2=0.由此能求出求出所有满足条件的点P的坐标及对应的直线方程.
点评:本题考查椭圆C的方程的求法,探究椭圆C上是否存在点P,使得当直线l绕点F转到某一位置时,有 成立.若存在,求出所有满足条件的点P的坐标及对应的直线方程;若不存在,请说明理由.综合性强,难度大,有一定的探索性,对数学思维能力要求较高,是高考的重点.解题时要认真审题,仔细解答.
成立.若存在,求出所有满足条件的点P的坐标及对应的直线方程;若不存在,请说明理由.综合性强,难度大,有一定的探索性,对数学思维能力要求较高,是高考的重点.解题时要认真审题,仔细解答.
 ,l:y=x-c,
,l:y=x-c,∴
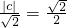 ,∴c=1.
,∴c=1.∵e=
 ,∴
,∴ ,∴b2=1.
,∴b2=1.∴椭圆C的方程为
 .
.(2)设A(x1,y1),B(x2,y2),P(x0,y0)设y=k(x-1)(k≠0)
由
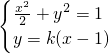 ,消去y得(1+2k2)x2-4k2x+2k2-2=0.
,消去y得(1+2k2)x2-4k2x+2k2-2=0.∴
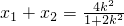 ,
,∴
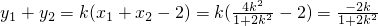 .
.∵
 ,
,∴x0=
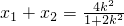 ,
,∴y0=
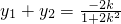 .
.将P点坐标代入椭圆得
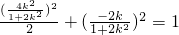 ,
,∴
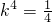 ,∴
,∴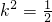 ,
,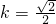 .
.当
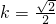 时,
时,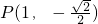 ,直线
,直线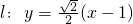 ,
,当
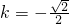 时,
时,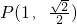 ,直线
,直线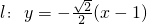 .
.分析:(1)由O到直线l的距离为
 ,l:y=x-c,知
,l:y=x-c,知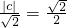 ,c=1.由e=
,c=1.由e= ,知
,知 ,b2=1.由此能求出椭圆C的方程.
,b2=1.由此能求出椭圆C的方程.(2)设A(x1,y1),B(x2,y2),P(x0,y0)设y=k(x-1)(k≠0)由
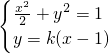 ,得(1+2k2)x2-4k2x+2k2-2=0.由此能求出求出所有满足条件的点P的坐标及对应的直线方程.
,得(1+2k2)x2-4k2x+2k2-2=0.由此能求出求出所有满足条件的点P的坐标及对应的直线方程.点评:本题考查椭圆C的方程的求法,探究椭圆C上是否存在点P,使得当直线l绕点F转到某一位置时,有
 成立.若存在,求出所有满足条件的点P的坐标及对应的直线方程;若不存在,请说明理由.综合性强,难度大,有一定的探索性,对数学思维能力要求较高,是高考的重点.解题时要认真审题,仔细解答.
成立.若存在,求出所有满足条件的点P的坐标及对应的直线方程;若不存在,请说明理由.综合性强,难度大,有一定的探索性,对数学思维能力要求较高,是高考的重点.解题时要认真审题,仔细解答. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的离心率e=
的离心率e= ,过点A(0,-b)和B(a,0)的直线与原点的距离为
,过点A(0,-b)和B(a,0)的直线与原点的距离为 ,求椭圆的标准方程。
,求椭圆的标准方程。 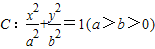 的离心率e=
的离心率e=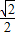 ,过右焦点F的直线l与椭圆C相交于A、B两点,当直线l的斜率为1时,坐标原点O到直线l的距离为
,过右焦点F的直线l与椭圆C相交于A、B两点,当直线l的斜率为1时,坐标原点O到直线l的距离为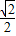 .
.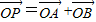 成立?若存在,求出所有满足条件的点P的坐标及对应的直线方程;若不存在,请说明理由.
成立?若存在,求出所有满足条件的点P的坐标及对应的直线方程;若不存在,请说明理由.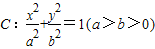 的离心率e=
的离心率e=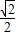 ,过右焦点F的直线l与椭圆C相交于A、B两点,当直线l的斜率为1时,坐标原点O到直线l的距离为
,过右焦点F的直线l与椭圆C相交于A、B两点,当直线l的斜率为1时,坐标原点O到直线l的距离为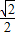 .
.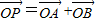 成立?若存在,求出所有满足条件的点P的坐标及对应的直线方程;若不存在,请说明理由.
成立?若存在,求出所有满足条件的点P的坐标及对应的直线方程;若不存在,请说明理由.