题目内容
已知复数z=(x-1)+(2x-1)i的模小于| 10 |
分析:写出复数的模长的表示形式,关键题意得到不等式,整理成关于x的二次不等式,进行因式分解求出结果.
解答:解:∵复数z=(x-1)+(2x-1)i的模小于
∴
<
,
∴(x-2)(5x+4)<0
∴-
<x<2,
∴实数x的取值范围是(-
,2)
故答案为:(-
,2)
| 10 |
∴
| (x-1)2+(2x-1)2 |
| 10 |
∴(x-2)(5x+4)<0
∴-
| 4 |
| 5 |
∴实数x的取值范围是(-
| 4 |
| 5 |
故答案为:(-
| 4 |
| 5 |
点评:本题考查复数求模长的问题,与一元二次不等式结合,解题的关键是表示出模长,写出不等式,解不等式,注意运算不要出错.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
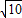 ,则实数x的取值范围是 .
,则实数x的取值范围是 .