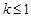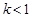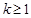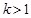题目内容
对于函数 ,如果存在锐角
,如果存在锐角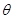 使得
使得 的图象绕坐标原点逆时针旋转角
的图象绕坐标原点逆时针旋转角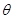 ,所得曲线仍是一函数,则称函数
,所得曲线仍是一函数,则称函数 具备角
具备角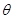 的旋转性,下列函数具有角
的旋转性,下列函数具有角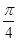 的旋转性的是
的旋转性的是
 ,如果存在锐角
,如果存在锐角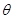 使得
使得 的图象绕坐标原点逆时针旋转角
的图象绕坐标原点逆时针旋转角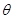 ,所得曲线仍是一函数,则称函数
,所得曲线仍是一函数,则称函数 具备角
具备角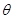 的旋转性,下列函数具有角
的旋转性,下列函数具有角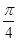 的旋转性的是
的旋转性的是A. | B.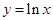 | C.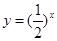 | D.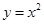 |
C
试题分析:若函数f(x)逆时针旋转
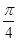 角后所得曲线仍是一函数,
角后所得曲线仍是一函数,则函数f(x)的图象与任一斜率为1的直线y=x+b均不能有两个以上的交点
A中函数
 与直线y=x有两个交点,不满足要求;
与直线y=x有两个交点,不满足要求;B中函数y=lnx与直线y=x-1有两个交点,不满足要求;
C中函数
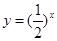 与直线y=x+b均有且只有一个交点,满足要求;
与直线y=x+b均有且只有一个交点,满足要求;D中函数y=x2与直线y=x有两个交点,不满足要求;故选C.
点评:本题考查的知识点是函数的定义,其中根据函数的定义分析出函数f(x)的图象与任一斜率为1的直线y=x+b均不能有两个以上的交点,是解答本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
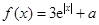 (
(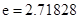 是自然对数的底数)的最小值为
是自然对数的底数)的最小值为 .
.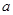 的值;
的值;
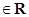 且
且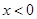 ,试解关于
,试解关于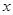 的不等式
的不等式  ;
;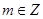 且
且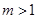 .若存在实数
.若存在实数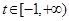 ,使得对任意的
,使得对任意的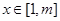 ,都有
,都有 ,试求
,试求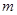 的最大值.
的最大值.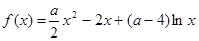 ,
,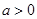 .
.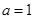 ,求函数
,求函数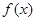 的极值;
的极值;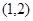 上有极值,求
上有极值,求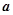 的取值范围.
的取值范围. 的图象如图所示,则
的图象如图所示,则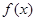 的解析式可能是 ( )
的解析式可能是 ( ) 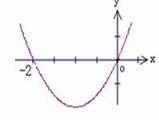
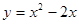
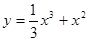
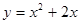
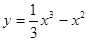
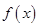 满足
满足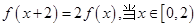 时,
时,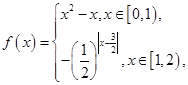 若
若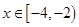 时,
时,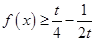 恒成立,则实数t的取值范围是
恒成立,则实数t的取值范围是



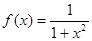
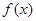 的奇偶性;
的奇偶性;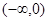 上是增函数还是减函数?证明你的结论.
上是增函数还是减函数?证明你的结论.
 (如图),考虑到防洪堤坚固性及石块用料等因素,设计其横断面要求面积为
(如图),考虑到防洪堤坚固性及石块用料等因素,设计其横断面要求面积为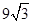 平方米,且高度不低于
平方米,且高度不低于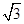 米,设防洪堤横断面的腰长为
米,设防洪堤横断面的腰长为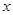 米,外周长(梯形的上底线段BC与两腰长的和)为
米,外周长(梯形的上底线段BC与两腰长的和)为 米.
米.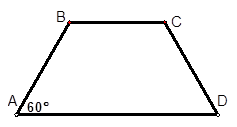
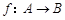 ,其中
,其中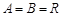 ,对应法则
,对应法则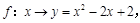 若对实数
若对实数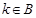 ,在集合A中不存在原象,则k的取值范围是 ( )
,在集合A中不存在原象,则k的取值范围是 ( )