题目内容
【题目】(本题16分)某乡镇为了进行美丽乡村建设,规划在长为10千米的河流OC的一侧建一条观光带,观光带的前一部分为曲线段OAB,设曲线段OAB为函数![]() ,
,![]() (单位:千米)的图象,且曲线段的顶点为
(单位:千米)的图象,且曲线段的顶点为![]() ;观光带的后一部分为线段BC,如图所示.
;观光带的后一部分为线段BC,如图所示.
(1)求曲线段OABC对应的函数![]() 的解析式;
的解析式;
(2)若计划在河流OC和观光带OABC之间新建一个如图所示的矩形绿化带MNPQ,绿化带由线段MQ,QP, PN构成,其中点P在线段BC上.当OM长为多少时,绿化带的总长度最长?

【答案】(1)  .
.
(2)当OM长为1千米时,绿化带的总长度最长![]() .
.
【解析】试题分析:(1)曲线段![]() 过点
过点![]() ,且最高点为
,且最高点为![]() ,可列出方程组,求解
,可列出方程组,求解![]() 的值,可得当
的值,可得当![]() 上函数的解析式,后一部分为线段
上函数的解析式,后一部分为线段![]() ,
,![]() ,可得
,可得![]() 上的解析式;(2)求出绿化带的总长度,可得二次函数即可得出结论.
上的解析式;(2)求出绿化带的总长度,可得二次函数即可得出结论.
试题解析:(1)因为曲线段OAB过点O,且最高点为![]()
 ,解得
,解得 (也可以设成顶点式)
(也可以设成顶点式)
所以,当![]() 时,
时,![]()
因为后一部分为线段BC,![]() ,当
,当![]() 时,
时,![]() ……6分
……6分
综上,
(2)设![]() ,则
,则![]()
由![]() , 得
, 得![]() ,
,
所以点![]()
所以,绿化带的总长度![]()
![]() ……13分
……13分
当![]() 时,
时,![]()
所以,当OM长为1千米时,绿化带的总长度最长

【题目】某地区某农产品近几年的产量统计如表:
年份 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代码 | 1 | 2 | 3 | 4 | 5 | 6 |
年产量 | 6.6 | 6.7 | 7 | 7.1 | 7.2 | 7.4 |
(1)根据表中数据,建立![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
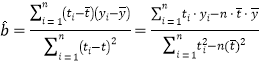 ,
,![]()
(2)若近几年该农产品每千克的价格![]() (单位:元)与年产量
(单位:元)与年产量![]() 满足的函数关系式为
满足的函数关系式为![]() ,且每年该农产品都能售完.
,且每年该农产品都能售完.
①根据(1)中所建立的回归方程预测该地区2019(![]() )年该农产品的产量;
)年该农产品的产量;
②当![]() 为何值时,销售额
为何值时,销售额![]() 最大?
最大?
【题目】某研究所计划利用“神舟十一号”飞船进行新产品搭载实验,计划搭载新产品![]() ,要根据该产品的研制成本、产品质量、搭载实验费用和预计产生收益来决定具体安排,通过调查,搭载每件产品有关数据如表:
,要根据该产品的研制成本、产品质量、搭载实验费用和预计产生收益来决定具体安排,通过调查,搭载每件产品有关数据如表:
因素 | 产品 | 产品 | 备注 |
研制成本、搭载费用之和/万元 | 20 | 30 | 计划最大投资 |
金额300万元产品质量/千克 | 10 | 5 | 最大搭载 |
质量110千克预计收益/万元 | 80 | 60 | —— |
则使总预计收益达到最大时, ![]() 两种产品的搭载件数分别为( )
两种产品的搭载件数分别为( )
A. 9,4 B. 8,5 C. 9,5 D. 8,4
【题目】下表数据为某地区某种农产品的年产量![]() (单位:吨)及对应销售价格
(单位:吨)及对应销售价格![]() (单位:千元/吨).
(单位:千元/吨).
| 1 | 2 | 3 | 4 | 5 |
| 70 | 65 | 55 | 38 | 22 |
(1)若![]() 与
与![]() 有较强的线性相关关系,根据上表提供的数据,用最小二乘法求出
有较强的线性相关关系,根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)若该农产品每吨的成本为13.1千元,假设该农产品可全部卖出,利用上问所求的回归方程,预测当年产量为多少吨时,年利润![]() 最大?
最大?
(参考公式:回归直线方程为![]() ,其中
,其中 )
)



