题目内容
(1)证明对数的换底公式: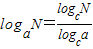 (其中a>0,a≠1,N>0,c>0,c≠1).
(其中a>0,a≠1,N>0,c>0,c≠1).(2)设a,b均为不等于1的正数,证明:
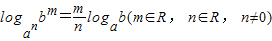 .
.
【答案】分析:(1)设logaN=b,则ab=N,两端同时取以c为底的对数,整理即可证得结论;
(2)利用(1)中的换底公式即可证得结论.
解答:证明:(1)∵a>0,a≠1,N>0,c>0,c≠1,
设logaN=b,
则ab=N,
∴logcN= =blogca,
=blogca,
∴ =
= =b,
=b,
∴logaN= ;
;
(2)∵a,b均为不等于1的正数,
由换底公式得, =
=
∴ =
= =
= logab.
logab.
点评:本题考查对数换底公式的证明与应用,利用指数式与对数式的互化是证明换底公式的基础,考查推理论证能力,属于基础题.
(2)利用(1)中的换底公式即可证得结论.
解答:证明:(1)∵a>0,a≠1,N>0,c>0,c≠1,
设logaN=b,
则ab=N,
∴logcN=
 =blogca,
=blogca,∴
 =
= =b,
=b,∴logaN=
 ;
;(2)∵a,b均为不等于1的正数,
由换底公式得,
 =
=
∴
 =
= =
= logab.
logab.点评:本题考查对数换底公式的证明与应用,利用指数式与对数式的互化是证明换底公式的基础,考查推理论证能力,属于基础题.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
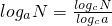 (其中a>0,a≠1,N>0,c>0,c≠1).
(其中a>0,a≠1,N>0,c>0,c≠1).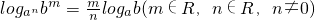 .
.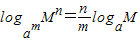 (a>0,且a≠1;M>0,m≠0).
(a>0,且a≠1;M>0,m≠0).