题目内容
若F1、F2分别为双曲线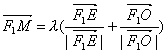 )(λ>0).
)(λ>0).(Ⅰ)求此双曲线的离心率;
(Ⅱ)若此双曲线过点(![]() ),直线l过其右焦点且与右支交于P、Q两点,若线段PQ的中点R在直线x=t(t≤1)上的射影C满足PC⊥QC,求实数t的取值范围.
),直线l过其右焦点且与右支交于P、Q两点,若线段PQ的中点R在直线x=t(t≤1)上的射影C满足PC⊥QC,求实数t的取值范围.
解:(Ⅰ)![]() ,则
,则![]() ,则四边形EF1OM为平行四边形.又由
,则四边形EF1OM为平行四边形.又由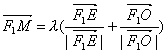 (λ>0),知点M在∠EF1O的角分线上,故四边形EF1OM为菱形,则=
(λ>0),知点M在∠EF1O的角分线上,故四边形EF1OM为菱形,则=![]() c,于是
c,于是![]() =2a+c,
=2a+c,
∴e=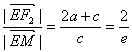 +1(e>1),解得e=2.
+1(e>1),解得e=2.
(Ⅱ)e=2,则b2=3a2,即![]() =1(a>0,b>0),
=1(a>0,b>0),
将(![]() )代入可得a2=1,故有x2
)代入可得a2=1,故有x2![]() =1.
=1.
设P点坐标(x1,y1),Q点坐标(x2,y2),
则![]() =e(x1
=e(x1![]() )=ex1-a=2x1-1,
)=ex1-a=2x1-1,
![]() =e(x2
=e(x2![]() )=2x2-1,∴|PQ|=2(x1+x2)-2.
)=2x2-1,∴|PQ|=2(x1+x2)-2.
若直线l斜率存在,设其方程为y=k(x-2),则由题设可知
|k|>![]() ,则由
,则由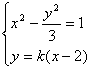 得(k2-3)x2-4k2x+(4k2+3)=0(|k|>
得(k2-3)x2-4k2x+(4k2+3)=0(|k|>![]() )
)
又PC⊥QC,∴|RC|=![]() |PQ|,则
|PQ|,则![]() [2(x1+x2)-2].
[2(x1+x2)-2].
∴t=![]() ,∴k2=
,∴k2=![]() ,又k2>3,∴
,又k2>3,∴![]() >3
>3![]() t<-1.
t<-1.
又当k不存在时,即PQ与x轴垂直,方程为x=2,∴R(2,0),
C(t,0),P(2,3),Q(2,-3),满足PC⊥QC,则易求得t=-1.综上可得:t≤-1.

练习册系列答案
相关题目
已知F1,F2分别为双曲
-
=1(a>0,b>0)的左、右焦点,P为双曲线左支上任一点,若
的最小值为8a,则双曲线的离心率e的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
| |PF2|2 |
| |PF1| |
| A、(1,+∞) |
| B、(0,3] |
| C、(1,3] |
| D、(0,2] |
 的左、右焦点,P为双曲线左支上任一点,若
的左、右焦点,P为双曲线左支上任一点,若 的最小值为8a,则双曲线的离心率e的取值范围是( )
的最小值为8a,则双曲线的离心率e的取值范围是( ) 的左、右焦点,P为双曲线左支上任一点,若
的左、右焦点,P为双曲线左支上任一点,若 的最小值为8a,则双曲线的离心率e的取值范围是( )
的最小值为8a,则双曲线的离心率e的取值范围是( ) 的左、右焦点,P为双曲线左支上任一点,若
的左、右焦点,P为双曲线左支上任一点,若 的最小值为8a,则双曲线的离心率e的取值范围是( )
的最小值为8a,则双曲线的离心率e的取值范围是( )