Question

【题目】已知曲线y=5,求:

(1)曲线上与直线y=2x-4平行的切线方程.

(2)求过点P(0,5),且与曲线相切的切线方程.

Answer 1

【答案】（1）16x-8y+25=0；（2）5x-4y+20=0.

【解析】

试题（1）求导数，利用曲线与直线y=2x﹣4平行，求出切点坐标，即可求出曲线与直线y=2x﹣4平行的切线的方程．

（2）设切点，可得切线方程，代入P，可得切点坐标，即可求出过点P（0，5）且与曲线相切的直线的方程．

试题解析：

(1)设切点为(x0,y0),由y=5,得y′=.

所以切线与y=2x-4平行,

所以=2,所以x0=,所以y0=.

则所求切线方程为y-=2,

即16x-8y+25=0.

(2)因为点P(0,5)不在曲线y=5上,

故需设切点坐标为M(x1,y1),

则切线斜率为.

又因为切线斜率为,

所以==,

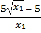所以2x1-2=x1,得x1=4.

所以切点为M(4,10),斜率为,

所以切线方程为y-10=(x-4),

即5x-4y+20=0.