题目内容
【题目】已知![]() 为平面上一点,
为平面上一点,![]() 为直线
为直线![]() :
:![]() 上任意一点,过点
上任意一点,过点![]() 作直线
作直线![]() 的垂线
的垂线![]() ,设线段
,设线段![]() 的中垂线与直线
的中垂线与直线![]() 交于点
交于点![]() ,记点
,记点![]() 的轨迹为
的轨迹为![]() .
.
(1)求轨迹![]() 的方程;
的方程;
(2)过点![]() 作互相垂直的直线
作互相垂直的直线![]() 与
与![]() ,其中直线
,其中直线![]() 与轨迹
与轨迹![]() 交于点
交于点![]() 、
、![]() ,直线
,直线![]() 与轨迹
与轨迹![]() 交于点
交于点![]() 、
、![]() ,设点
,设点![]() ,
,![]() 分别是
分别是![]() 和
和![]() 的中点,求
的中点,求![]() 的面积的最小值.
的面积的最小值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)利用轨迹与方程的思想,构造等量关系,求轨迹方程;
(2)用直线斜截式方程设直线方程与曲线方程联立,利用韦达定理求出点![]() ,
,![]() 坐标,可将
坐标,可将![]() 的面积表示为关于直线斜率的函数,利用函数性质求
的面积表示为关于直线斜率的函数,利用函数性质求![]() 的面积的最小值.
的面积的最小值.
(1)设点![]() 则
则![]() ,设
,设![]() 的中点为
的中点为![]() ,则
,则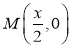 ,
,
且![]() 为
为![]() 的中垂线,
的中垂线,
当![]() 时,
时,![]()
即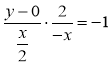 ,
,
∴![]()
当![]() 时,
时,![]() ,则
,则![]()
综上所述点![]() 的轨迹
的轨迹![]() 的方程为
的方程为![]() ;
;
(2)设直线![]() 的斜率为
的斜率为![]() ,
,
且![]() ,则直线
,则直线![]() 的斜率为
的斜率为![]() ,
,
∵直线![]() 与轨迹
与轨迹![]() 交于点
交于点![]() 、
、![]() ,直线
,直线![]() 与轨迹
与轨迹![]() 交于点
交于点![]() 、
、![]() ,
,
∴![]() ,
,
∴直线![]() 的方程为
的方程为![]() ,直线
,直线![]() 的方程为
的方程为![]() ,
,
设![]() ,联立直线
,联立直线![]() 与曲线
与曲线![]() 方程
方程
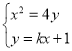
∴![]()
∴![]() ,
,
即![]() ,
,![]() ,
,
且点![]() 是
是![]() 的中点,
的中点,
∴![]()
同理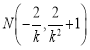
设点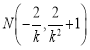 到直线
到直线![]() :
:![]() 的距离为
的距离为![]() ,
,
∴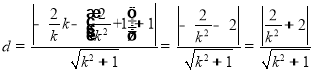 ,
,
![]() ,
,
∴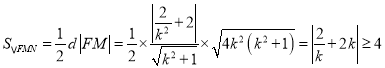 ,
,
∴![]() 的面积的最小值为
的面积的最小值为![]() .
.

【题目】某外卖平台为提高外卖配送效率,针对外卖配送业务提出了两种新的配送方案,为比较两种配送方案的效率,共选取50名外卖骑手,并将他们随机分成两组,每组25人,第一组骑手用甲配送方案,第二组骑手用乙配送方案.根据骑手在相同时间内完成配送订单的数量(单位:单)绘制了如下茎叶图:
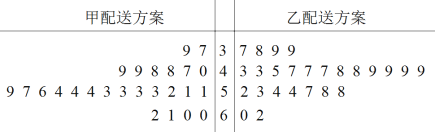
(1)根据茎叶图,求各组内25位骑手完成订单数的中位数,已知用甲配送方案的25位骑手完成订单数的平均数为52,结合中位数与平均数判断哪种配送方案的效率更高,并说明理由;
(2)设所有50名骑手在相同时间内完成订单数的平均数![]() ,将完成订单数超过
,将完成订单数超过![]() 记为“优秀”,不超过
记为“优秀”,不超过![]() 记为“一般”,然后将骑手的对应人数填入下面列联表;
记为“一般”,然后将骑手的对应人数填入下面列联表;
优秀 | 一般 | |
甲配送方案 | ||
乙配送方案 |
(3)根据(2)中的列联表,判断能否有![]() 的把握认为两种配送方案的效率有差异.
的把握认为两种配送方案的效率有差异.
附: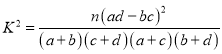 ,其中
,其中![]() .
.
| 0.05 | 0.010 | 0.005 |
| 3.841 | 6.635 | 7.879 |
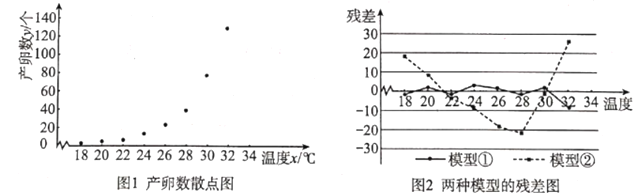
【题目】红铃虫(Pectinophora gossypiella)是棉花的主要害虫之一,其产卵数与温度有关.现收集到一只红铃虫的产卵数y(个)和温度x(℃)的8组观测数据,制成图1所示的散点图.现用两种模型①![]() ,②
,②![]() 分别进行拟合,由此得到相应的回归方程并进行残差分析,进一步得到图2所示的残差图.
分别进行拟合,由此得到相应的回归方程并进行残差分析,进一步得到图2所示的残差图.
根据收集到的数据,计算得到如下值:
|
|
|
|
|
|
|
25 | 2.89 | 646 | 168 | 422688 | 48.48 | 70308 |
表中![]() ;
;![]() ;
;![]() ;
;![]() ;
;
(1)根据残差图,比较模型①、②的拟合效果,应选择哪个模型?并说明理由;
(2)根据(1)中所选择的模型,求出y关于x的回归方程(系数精确到0.01),并求温度为34℃时,产卵数y的预报值.
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() )
)
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为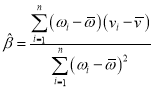 ,
,![]() .
.
【题目】为了调查某社区居民每天参加健身的时间,某机构在该社区随机采访男性、女性各50名,其中每人每天的健身时间不少于1小时称为“健身族”,否则称其为"非健身族”,调查结果如下:
健身族 | 非健身族 | 合计 | |
男性 | 40 | 10 | 50 |
女性 | 30 | 20 | 50 |
合计 | 70 | 30 | 100 |
(1)若居民每人每天的平均健身时间不低于70分钟,则称该社区为“健身社区”. 已知被随机采访的男性健身族,男性非健身族,女性健身族,女性非健身族每人每天的平均健分时间分別是1.2小时,0.8小时,1.5小时,0.7小时,试估计该社区可否称为“健身社区”?
(2)根据以上数据,能否在犯错误的概率不超过5%的情况下认为“健身族”与“性别”有关?
参考公式: 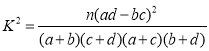 ,其中
,其中![]() .
.
参考数据:
| 0. 50 | 0. 40 | 0. 25 | 0. 05 | 0. 025 | 0. 010 |
| 0. 455 | 0. 708 | 1. 321 | 3. 840 | 5. 024 | 6. 635 |