题目内容
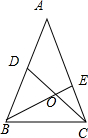
15.已知直线m⊥平面α,直线n在平面β内,给出下列三个命题:①“α∥β”是“m⊥n”的充分不必要条件;②“α⊥β”是“m∥n”的必要不充分条件;③“α⊥β”是“m⊥n”的充要条件.则其中真命题的个数为( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 对于①:若α∥β,则直线m⊥直线n,反之不成立;对于②:若m∥n,则α⊥β,反之不成立;对于“α⊥β”是“m⊥n”的既不充分也不必要条件.
解答 解:对于①:若α∥β,
∵直线m⊥平面α,∴直线m⊥平面β,
∵直线n在平面β内,∴直线m⊥直线n,反之不成立,所以①是真命题;
对于②:若m∥n,
∵直线m⊥平面α,∴直线n⊥平面α,
∵直线n在平面β内,∴α⊥β,反之不成立,所以②是真命题;
对于③:∵直线m⊥平面α,直线n在平面β内,
∴“α⊥β”是“m⊥n”的既不充分也不必要条件,所以③是假命题.
所以真命题的个数为2.
故选:C.
点评 本题考查命题真假的判断,是中档题,解题时要认真审题,注意空间中线线、线面、面面间的位置关系的合理运用.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
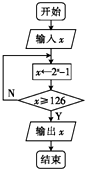
5.执行如图所示的程序框图,则输出的结果为( )
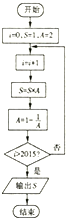

| A. | 2 | B. | 1 | C. | -1 | D. | -2 |
10.在数列{an}中,若存在一个确定的正整数T,对任意n∈N*满足an+T=an,则称{an}是周期数列,T叫做它的周期.已知数列{xn}满足x1=1,x2=a(a≤1),xn+2=|xn+1-xn|,若数列{xn}的周期为3,则{xn}的前2014项的和为( )
| A. | 1344 | B. | 1343 | C. | 1224 | D. | 1223 |
7. 如图所示的算法流程图中,若f(x)=lnx,g(x)=log2x,则h(4)的值等于( )
如图所示的算法流程图中,若f(x)=lnx,g(x)=log2x,则h(4)的值等于( )
 如图所示的算法流程图中,若f(x)=lnx,g(x)=log2x,则h(4)的值等于( )
如图所示的算法流程图中,若f(x)=lnx,g(x)=log2x,则h(4)的值等于( )| A. | 1 | B. | -1 | C. | 2 | D. | ln4 |