题目内容
已知函数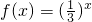 的反函数为g(x),则函数y=g(2x-x2)的单调递增区间为
的反函数为g(x),则函数y=g(2x-x2)的单调递增区间为
- A.(1,+∞)
- B.(-∞,1)
- C.(0,1)
- D.(1,2)
D
分析:先求出反函数g(x),通过换元求出y=g(2x-x2)=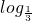 (2x-x2),确定此函数的定义域,然后在定义域的前提条件下根据2x-x2的单调性以及复合函数的单调性可求出所求.
(2x-x2),确定此函数的定义域,然后在定义域的前提条件下根据2x-x2的单调性以及复合函数的单调性可求出所求.
解答:∵函数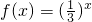 的反函数为g(x),
的反函数为g(x),
∴g(x)=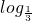 x,
x,
∴函数y=g(2x-x2)=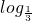 (2x-x2),
(2x-x2),
由2x-x2>0得0<x<2,即定义域为 (0,2),
x∈(0,1),2x-x2单调递增,此时y=g(2x-x2)=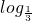 (2x-x2)单调递减;
(2x-x2)单调递减;
x∈(1,2)时,2x-x2单调递减,此时y=g(2x-x2)=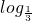 (2x-x2)单调递增.
(2x-x2)单调递增.
∴g(2x-x2)的单调递增区间为(1,2).
故选D.
点评:本题主要考查反函数的求法,以及复合函数的单调性,体现了整体的数学思想,定义域是单调区间的前提,属于基础题.
分析:先求出反函数g(x),通过换元求出y=g(2x-x2)=
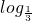 (2x-x2),确定此函数的定义域,然后在定义域的前提条件下根据2x-x2的单调性以及复合函数的单调性可求出所求.
(2x-x2),确定此函数的定义域,然后在定义域的前提条件下根据2x-x2的单调性以及复合函数的单调性可求出所求.解答:∵函数
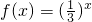 的反函数为g(x),
的反函数为g(x),∴g(x)=
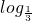 x,
x,∴函数y=g(2x-x2)=
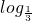 (2x-x2),
(2x-x2),由2x-x2>0得0<x<2,即定义域为 (0,2),
x∈(0,1),2x-x2单调递增,此时y=g(2x-x2)=
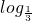 (2x-x2)单调递减;
(2x-x2)单调递减;x∈(1,2)时,2x-x2单调递减,此时y=g(2x-x2)=
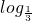 (2x-x2)单调递增.
(2x-x2)单调递增.∴g(2x-x2)的单调递增区间为(1,2).
故选D.
点评:本题主要考查反函数的求法,以及复合函数的单调性,体现了整体的数学思想,定义域是单调区间的前提,属于基础题.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
 的反函数是y=g(x),则g(x)在(0,+∞)上单调递增.
的反函数是y=g(x),则g(x)在(0,+∞)上单调递增.