题目内容
平面直角坐标系xOy内有向量 =(1,7),
=(1,7), =(5,1),
=(5,1), =(2,1),点Q为直线OP上一动点.
=(2,1),点Q为直线OP上一动点.
(1)当 ·
· 取得最小值时,求
取得最小值时,求 坐标;
坐标;
(2)当点Q满足(1)中条件时,求cos∠AQB的值.
【答案】
(1)当y=2时,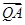 ·
·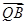 有最小值-8,此时
有最小值-8,此时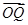 =(4,2).(2)-
=(4,2).(2)-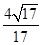 .
.
【解析】
试题分析:(1)设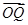 =(x,y),∴点Q在直线
=(x,y),∴点Q在直线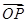 上,
上,
∴向量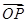 与
与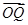 共线,又
共线,又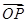 =(2,1),
=(2,1),
∴x-2y=0,即x=2y,∴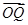 =(2y,y),
=(2y,y),
又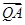 =
=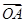 -
-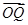 =(1-2y,7-y),
=(1-2y,7-y),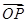 =(5-2y,1-y)
=(5-2y,1-y)
∴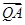 ·
·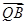 =(1-2y)·(5-2y)+(7-y)·(1-y)=5y2-20y+12=5(y-2)2-8,
=(1-2y)·(5-2y)+(7-y)·(1-y)=5y2-20y+12=5(y-2)2-8,
故当y=2时,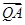 ·
·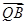 有最小值-8,此时
有最小值-8,此时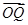 =(4,2).
=(4,2).
(2)由(1)知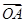 =(-3,5),
=(-3,5),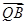 =(1,-1),
=(1,-1),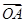 ·
·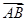 =-8,|
=-8,|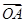 |=
|=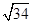 ,
,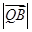 =
=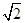 .
.
∴cos∠AQB=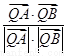 =-
=-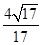 .
.
考点:平面向量的线性运算,平面向量的数量积,平面向量的坐标计算,二次函数的图象和性质。
点评:中档题,本题综合考查平面向量的线性运算,平面向量的数量积,平面向量的坐标计算,二次函数的图象和性质,对学生的计算能力有较高要求。向量的夹角公式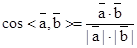 。平面向量模的计算,往往“化模为方”,转化成向量的运算。
。平面向量模的计算,往往“化模为方”,转化成向量的运算。

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
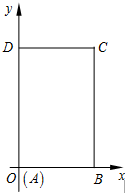 如图,在平面直角坐标系xOy中,已知矩形ABCD的两边AB,CD分别落在x轴、y轴的正半轴上,且AB=2,AD=4,点A与坐标原点重合.现将矩形折叠,使点A落在线段DC上,若折痕所在的直线的斜率为k,试写出折痕所在直线的方程及k的范围.
如图,在平面直角坐标系xOy中,已知矩形ABCD的两边AB,CD分别落在x轴、y轴的正半轴上,且AB=2,AD=4,点A与坐标原点重合.现将矩形折叠,使点A落在线段DC上,若折痕所在的直线的斜率为k,试写出折痕所在直线的方程及k的范围.