Question

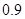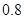某学生语、数、英三科考试成绩，在一次考试中排名全班第一的概率：语文为，数学为，英语为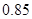，问一次考试中

（Ⅰ）三科成绩均未获得第一名的概率是多少？

（Ⅱ）恰有一科成绩未获得第一名的概率是多少

 

Answer 1

【答案】

（Ⅰ）三科成绩均未获得第一名的概率是 

（Ⅱ）恰有一科成绩未获得第一名的概率是

【解析】

试题分析：解：分别记该生语、数、英考试成绩排名全班第一的事件为，

则  

（Ⅰ）

答：三科成绩均未获得第一名的概率是 

（Ⅱ）（）

答：恰有一科成绩未获得第一名的概率是

考点：本题主要考查离散型随机变量的概率计算。

点评：注意事件的相互独立性，利用公式加以计算。