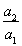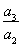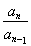题目内容
如果数列a1,
,
,…,
,…是首项为1,公比为-
的等比数列,则a5等于
| a2 |
| a1 |
| a3 |
| a2 |
| an |
| an-1 |
| 2 |
32
32
.分析:由已知可得
=(-
)n-1,a1=1,然后利用叠乘法a5=
•
•
•
•a1可求
| an |
| an-1 |
| 2 |
| a5 |
| a4 |
| a4 |
| a3 |
| a3 |
| a2 |
| a2 |
| a1 |
解答:解:∵a1,
,
,…,
,…是首项为1,公比为-
的等比数列
∴
=(-
)n-1,a1=1
∴
=-
,
=2,
=-2
,
=4
∴a5=
•
•
•
•a1=4×(-2
)×2×(-
)×1=32
故答案为:32
| a2 |
| a1 |
| a3 |
| a2 |
| an |
| an-1 |
| 2 |
∴
| an |
| an-1 |
| 2 |
∴
| a2 |
| a1 |
| 2 |
| a3 |
| a2 |
| a4 |
| a3 |
| 2 |
| a5 |
| a4 |
∴a5=
| a5 |
| a4 |
| a4 |
| a3 |
| a3 |
| a2 |
| a2 |
| a1 |
| 2 |
| 2 |
故答案为:32
点评:本题主要考查了等比数列的通项公式及叠乘法在数列的项的求解中的应用

练习册系列答案
相关题目
如果数列a1,a2,a3,…,an,…是等差数列,那么下列数列中不是等差数列的是:( )
| A、a1+x,a2+x,a3+x,…,an+x, | ||||||||
| B、ka1,ka2,ka3,…,kan, | ||||||||
C、
| ||||||||
| D、a1,a4,a7,…a3n-2, |