题目内容
已知函数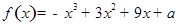 在区间[-2,2]的最大值为20,求它在该区间的最小值。
在区间[-2,2]的最大值为20,求它在该区间的最小值。
最小值为-7.
解析试题分析:因为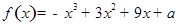 ,所以
,所以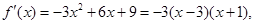
令 ,
,
所以该函数在 上单调递减,在
上单调递减,在 上单调递增,
上单调递增,
所以函数在 处取到最小值,
处取到最小值,
而
所以该函数在区间[-2,2]的最大值为 ,
,
所以该函数在区间[-2,2]的最小值为
考点:本小题主要考查函数的极值、最值。
点评:解决此类问题的关键是利用导数研究单调性、极值、最值等,要交代清楚函数的单调性,必要时可以借助表格进行说明.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
 .
. 在
在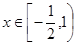 上的最大值为
上的最大值为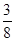 ,求实数
,求实数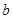 的值;
的值; ,都有
,都有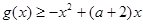 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;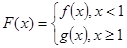 ,对任意给定的正实数
,对任意给定的正实数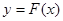 上是否存在两点
上是否存在两点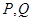 ,使得
,使得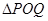 是以
是以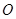 (
( 轴上?请说明理由.
轴上?请说明理由.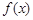 的导函数是
的导函数是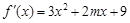 ,
,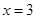 处取得极值,且
处取得极值,且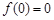 ,
, 上的最大值为
上的最大值为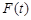 ,若对任意的
,若对任意的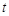
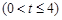 总有
总有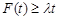 成立,求
成立,求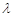 的取值范围;
的取值范围;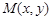 是曲线
是曲线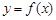 上的任意一点.当
上的任意一点.当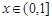 时,求直线OM斜率的最
时,求直线OM斜率的最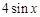 的大小关系,并说明理由.
的大小关系,并说明理由.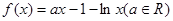
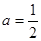 时,求函数在
时,求函数在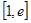 上的最大值和最小值;
上的最大值和最小值;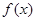 在
在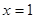 处取得极值,不等式
处取得极值,不等式 对
对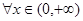 恒成立,求实数
恒成立,求实数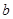 的取值范围。
的取值范围。 .
. 的单调区间;
的单调区间; ,使得
,使得 成立,求实数
成立,求实数 的取值范围.
的取值范围.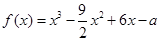 .
.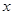 ,
,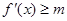 恒成立,求
恒成立,求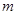 的最大值;
的最大值;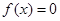 有且仅有一个实根,求
有且仅有一个实根,求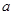 的取值范围.
的取值范围. 。(Ⅰ)若函数
。(Ⅰ)若函数 在
在 处与直线
处与直线 相切,①求实数
相切,①求实数 ,b的值;②求函数
,b的值;②求函数 上的最大值;(Ⅱ)当
上的最大值;(Ⅱ)当 时,若不等式
时,若不等式 对所有的
对所有的 都成立,求实数m的取值范围。)
都成立,求实数m的取值范围。)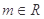 ,函数
,函数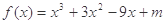 .
.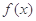 的极值(用含
的极值(用含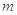 的式子表示);
的式子表示);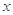 轴有3个不同交点,求
轴有3个不同交点,求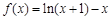 .
. 的单调递减区间;
的单调递减区间;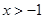 ,证明:
,证明: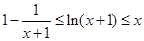 .
.