题目内容
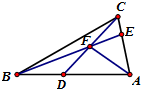 如图,△ABC中,AD=2DB,AE=3EC,CD与BE交于F,若
如图,△ABC中,AD=2DB,AE=3EC,CD与BE交于F,若| AF |
| AB |
| AC |
分析:过点F作FM∥AC、FN∥AB,分别交AB、AC于点M、N.由平行线分线段成比例,结合AD=2DB且AE=3EC,证出AM=
AB且AN=
AC,最后由平面向量基本定理和向量的加法法则,即可算出x、y的值.
| 1 |
| 3 |
| 1 |
| 2 |
解答:解: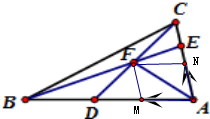 过点F作FM∥AC、FN∥AB,分别交AB、AC于点M、N
过点F作FM∥AC、FN∥AB,分别交AB、AC于点M、N
∵FM∥AC,∴
=
且
=
∵AD=2DB,AE=3EC,
∴AD=
AB,AE=
AC.由此可得AM=
AB
同理可得AN=
AC
∵四边形AMFN是平行四边形
∴由向量加法法则,得
=
+
∵
=x
+y
,
∴根据平面向量基本定理,可得x=
,y=
故选:A
 过点F作FM∥AC、FN∥AB,分别交AB、AC于点M、N
过点F作FM∥AC、FN∥AB,分别交AB、AC于点M、N∵FM∥AC,∴
| FM |
| AC |
| DM |
| AD |
| FM |
| AE |
| BM |
| AB |
∵AD=2DB,AE=3EC,
∴AD=
| 2 |
| 3 |
| 3 |
| 4 |
| 1 |
| 3 |
同理可得AN=
| 1 |
| 2 |
∵四边形AMFN是平行四边形
∴由向量加法法则,得
| AF |
| 1 |
| 3 |
| AB |
| 1 |
| 2 |
| AC |
∵
| AF |
| AB |
| AC |
∴根据平面向量基本定理,可得x=
| 1 |
| 3 |
| 1 |
| 2 |
故选:A
点评:本题在三角形中给出边的三等分点和四等分点,求向量的线性表示式.着重考查了平行线的性质、向量的加法法则和平面向量基本定理及其应用等知识,属于中档题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
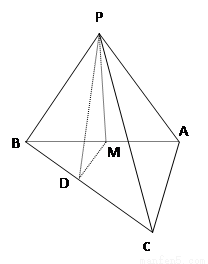
 如图,△ABC中,∠A=90°,AB=4,AC=3,平面ABC外一点P在平面ABC内的射影是AB中点M,二面角P-AC-B的大小为45°.
如图,△ABC中,∠A=90°,AB=4,AC=3,平面ABC外一点P在平面ABC内的射影是AB中点M,二面角P-AC-B的大小为45°. 如图在△ABC中,AB⊥AC,
如图在△ABC中,AB⊥AC,