题目内容
改革开放以来,我国高等教育事业有了突飞猛进的发展,有人记录了某村 到
到 年十年间每年考入大学的人数.为方便计算,
年十年间每年考入大学的人数.为方便计算, 年编号为
年编号为 ,
, 年编号为
年编号为 ,…,
,…, 年编号为
年编号为 .数据如下:
.数据如下:
(1)从这 年中随机抽取两年,求考入大学的人数至少有
年中随机抽取两年,求考入大学的人数至少有 年多于
年多于 人的概率;
人的概率;
(2)根据前 年的数据,利用最小二乘法求出
年的数据,利用最小二乘法求出 关于
关于 的回归方程
的回归方程 ,并计算第
,并计算第 年的估计值和实际值之间的差的绝对值。
年的估计值和实际值之间的差的绝对值。

 到
到 年十年间每年考入大学的人数.为方便计算,
年十年间每年考入大学的人数.为方便计算, 年编号为
年编号为 ,
, 年编号为
年编号为 ,…,
,…, 年编号为
年编号为 .数据如下:
.数据如下:年份( ) ) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
人数( ) ) | 3 | 5 | 8 | 11 | 13 | 14 | 17 | 22 | 30 | 31 |
 年中随机抽取两年,求考入大学的人数至少有
年中随机抽取两年,求考入大学的人数至少有 年多于
年多于 人的概率;
人的概率;(2)根据前
 年的数据,利用最小二乘法求出
年的数据,利用最小二乘法求出 关于
关于 的回归方程
的回归方程 ,并计算第
,并计算第 年的估计值和实际值之间的差的绝对值。
年的估计值和实际值之间的差的绝对值。
(1)
(2)则第8年的估计值和真实值之间的差的绝对值为

(2)则第8年的估计值和真实值之间的差的绝对值为

(1)设考入大学人数至少有1年多于15人的事件为A则P(A)=1- =
= (4’)
(4’)
(2)由已知数据得 =3,
=3, =8,
=8, =3+10+24+44+65=146
=3+10+24+44+65=146 =1+4+9+16+25=55(7’)
=1+4+9+16+25=55(7’)
则 =
= ,
, (9’)
(9’)
则回归直线方程为y=2.6x+0.2 (10’)
则第8年的估计值和真实值之间的差的绝对值为
 =
= (4’)
(4’)(2)由已知数据得
 =3,
=3, =8,
=8, =3+10+24+44+65=146
=3+10+24+44+65=146 =1+4+9+16+25=55(7’)
=1+4+9+16+25=55(7’)则
 =
= ,
, (9’)
(9’)则回归直线方程为y=2.6x+0.2 (10’)
则第8年的估计值和真实值之间的差的绝对值为


练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
 ,计算(结果保留到小数点后面第2位)
,计算(结果保留到小数点后面第2位)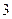 次预报准确的概率
次预报准确的概率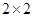 列联表进行独立性检验,经计算
列联表进行独立性检验,经计算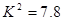 ,则所得到的统计学结论是:有______的把握认为“爱好该项运动与性别有关”.附:
,则所得到的统计学结论是:有______的把握认为“爱好该项运动与性别有关”.附:
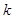
 ,从中任取一个.
,从中任取一个. ,至少存在另一个正整数
,至少存在另一个正整数 ,且
,且 ,使得
,使得 ”的概率;
”的概率; 为组成该数的相同数字的个数的最大值,求
为组成该数的相同数字的个数的最大值,求 装置就可以正常工作。每套系统都由三种电子模块T1,T2,T3组成(如图所示已知T1,T2,T3正常工作的概率都是
装置就可以正常工作。每套系统都由三种电子模块T1,T2,T3组成(如图所示已知T1,T2,T3正常工作的概率都是 ,且T1,T2,T3能否正常工作相互独立.(注:对每一套系统或每一种电子模块而言,只要有电流通过就能正常工作.)
,且T1,T2,T3能否正常工作相互独立.(注:对每一套系统或每一种电子模块而言,只要有电流通过就能正常工作.)
 ;
; ,求
,求 的分布列和期望.
的分布列和期望.
 ,则
,则 的值为( )
的值为( )


