Question

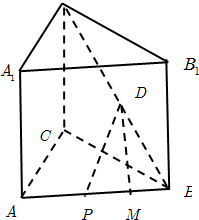如图，在正三棱柱ABC-A₁B₁C₁中，AB=2，AA1=

6

，D为C₁B的中点．
①当P为AB中点时，证明：DP∥平面ACC₁A₁；
②若AM=3MB，求异面直线DM与AC所成的角．

Answer 1

分析：①连接DP、AC₁，在△ABC₁中根据中位线定理，得DP∥AC₁，结合线面平行的判定定理，得DP∥平面ACC₁A₁；
②建立空间直角坐标系，转化为向量

CA

与

DM

的夹角求解，求出向量坐标，利用向量夹角公式即可求得，根据向量夹角与异面角的关系即可得到答案．

解答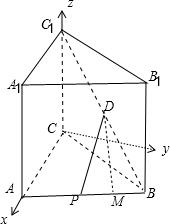：①证明：连接DP、AC₁，
∵△ABC₁中，P、D分别为AB、BC₁中点，
∴DP∥AC₁，
∵AC₁?平面ACC₁A₁，DP?平面ACC₁A₁，
∴DP∥平面ACC₁A₁；
②如图建立空间直角坐标系，则C（0，0，0），A（2，0，0），M（

5

4

，

3 3

4

，0），D（

1

2

，

3

2

，

6

2

），
所以

CA

=（2，0，0），

DM

=（

3

4

，

3

4

，-

6

2

），
所以cos＜

CA

，

DM

＞=

CA • DM

| CA || DM |

=

2× 3 4

2× ( 3 4 )2+( 3 4 )2+(- 6 2 )2

=

1

2

，
所以＜

CA

，

DM

＞=60°，
故异面直线DM与AC所成的角为60°．

点评：本题在直三棱柱中证明线面平行、异面直线所成的角，着重考查了线面平行的判定、异面角等知识，属于中档题，用向量法求解注意向量夹角与异面直线所成角的关系，异面角的范围为（0，

π

2

]．