题目内容

定义域为R的偶函数，当>0时，．若方程恰有5个不同的实数解，求的取值范围，并求出函数的解析式．

解：因为为偶函数，所以的5个解中必有1个解在y轴上，

且当>0时的图像与轴恰有两个不同的交点．

       下面研究>0时的情况．

       当<0时，为单调增函数，当0时，，

当时，，所以与轴仅有一个交点．

当=0时，与轴仅有一个交点．

    所以必须满足>0．

    ，令，得

当时，，单调递增；当时，，

单调递减．

    所以在处取到极大值．

    又当时，；当时，．

    要使>0时，与轴有两个交点，应满足>0，解得0<，

    设<0，一>0，，

    ∴

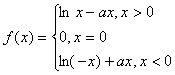
练习册系列答案
相关题目
已知定义域为R的偶函数f（x）在区间[0，+∞）上是增函数，若f（1）＜f（lgx），则实数x的取值范围是
(0，
1
10
)∪(10，+∞)
(0，
1
10
)∪(10，+∞)
．
已知f（x）是定义域为R的偶函数，当x＞0时解析式为f（x）=x2+x，则当x＜0时，f（x）=
x2-x
x2-x
．
定义域为R的偶函数f（x）满足对?∈R，有f（x+2）=f（x）-f（1），且当x∈[2，3]时，f（x）=-2x2+12x-18，若方程f（x）=loga（x+1）在（0，+∞）上恰有三个不同的根，则a的取值范围是（　　）
（2012•黄浦区二模）已知函数y=f（x）是定义域为R的偶函数，且对x∈R，恒有f（1+x）=f（1-x）．又当x∈[0，1]时，f（x）=x．
（1）当x∈[-1，0]时，求f（x）的解析式；
（2）求证：函数y=f（x）（x∈R）是以T=2为周期的周期函数；
（3）解答本小题考生只需从下列三个问题中选择一个写出结论即可（无需写解题步骤）．注意：考生若选择多于一个问题解答，则按分数最低一个问题的解答正确与否给分．
①当x∈[2n-1，2n]（n∈Z）时，求f（x）的解析式．
②当x∈[2n-1，2n+1]（其中n是给定的正整数）时，若函数y=f（x）的图象与函数y=kx的图象有且仅有两个公共点，求实数k的取值范围．
③当x∈[0，2n]（n是给定的正整数且n≥3）时，求f（x）的解析式．
定义域为R的偶函数f（x）满足?x∈R，有f（x+2）=f（x）-f（1），且当x∈[2，3]时，f（x）=-2x2+12x-18．若函数y=f（x）-loga（x+1）至少有三个零点，则a的取值范围是（　　）
A、（0，
2
2
）
B、（0，
3
3
）
C、（0，
5
5
）
D、（0，
6
6
）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网