题目内容
（选修4-5：不等式选讲）
已知a，b，c为正数，且a2+a2+c2=14，试求a+2b+3c的最大值．
解：设向量
，
，可得
，
=
，
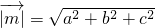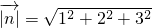=a+2b+3c
∵=
•
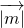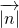cosθ，|cosθ|≤1（θ为向量
、
的夹角）
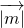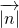∴||≤•，可得|a+2b+3c|≤
•
∵a2+a2+c2=14，
∴|a+2b+3c|≤14，可得-14≤a+2b+3c≤14
当且仅当a：b：c=1：2：3时，即a=1，b=2，c=3时，a+2b+3c取最大值14．
分析：设向量，，结合数量积的性质||≤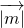•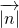，可得|a+2b+3c|≤•，即|a+2b+3c|≤14，由此可得a+2b+3c的最大值．
点评：本题已知a、b、c三个数的平方和的值，求a+2b+3c的最大值．着重考查了空间向量数量积的性质和柯西不等式求最值等知识，属于基础题．
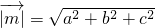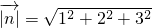，，可得，=，=a+2b+3c∵
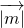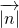=•cosθ，|cosθ|≤1（θ为向量、的夹角）∴|
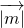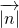|≤•，可得|a+2b+3c|≤•∵a2+a2+c2=14，
∴|a+2b+3c|≤14，可得-14≤a+2b+3c≤14
当且仅当a：b：c=1：2：3时，即a=1，b=2，c=3时，a+2b+3c取最大值14．
分析：设向量
，，结合数量积的性质||≤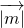•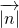，可得|a+2b+3c|≤•，即|a+2b+3c|≤14，由此可得a+2b+3c的最大值．点评：本题已知a、b、c三个数的平方和的值，求a+2b+3c的最大值．着重考查了空间向量数量积的性质和柯西不等式求最值等知识，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
本题包括（1）、（2）、（3）、（4）四小题，请选定其中两题，并在答题卡指定区域内答，