题目内容
如图，圆柱的轴截面ABCD为正方形，O′、O分别为上、下底面的圆心，E为上底面圆周上一点，已知∠DO′E=60°，圆柱侧面积等于16π．（1）求圆柱的体积V；
（2）求异面直线BE与DO所成角θ的大小．
分析：由题设条件可设圆柱的底面半径为r，则圆柱的高为2r，根据圆柱侧面积等于16π建立方程求出底面半径r，即可求得圆柱的高
（1）圆柱高与底面半径已知，故代入公式求体积即可；
（2）连接O′B，可证得角O′BE两异面直线所成的角，在三角形中求之即可．
（1）圆柱高与底面半径已知，故代入公式求体积即可；
（2）连接O′B，可证得角O′BE两异面直线所成的角，在三角形中求之即可．
解答：
解：（1）设圆柱的底面半径为r，由题意，得2πr×2r=16π
解得：r=2．∴V=πr2×2r=16π．
（2）连接O′B，由于O′B∥DO，
所以，∠EBO′即为BE与DO所成角θ，
过点E作圆柱的母线交下底面于点F，连接FB，FO，
由圆柱的性质，得△EFB为直角三角形，四边形EO′OF为矩形，BO′=DO=2
，
由∠DO′E=60°，由等角定理，得∠AOF=60°
所以，∠BOF=120°
可解得，BF=2
在Rt△EFB中，BE=
=2
由余弦定理，cosθ=
=
．
∴θ=arccos
．
解：（1）设圆柱的底面半径为r，由题意，得2πr×2r=16π解得：r=2．∴V=πr2×2r=16π．
（2）连接O′B，由于O′B∥DO，
所以，∠EBO′即为BE与DO所成角θ，
过点E作圆柱的母线交下底面于点F，连接FB，FO，
由圆柱的性质，得△EFB为直角三角形，四边形EO′OF为矩形，BO′=DO=2
| 5 |
由∠DO′E=60°，由等角定理，得∠AOF=60°
所以，∠BOF=120°
可解得，BF=2
| 3 |
在Rt△EFB中，BE=
| EF2+FB2 |
| 7 |
由余弦定理，cosθ=
| BE2+BO′2-EO′2 |
| 2×BO×EO′ |
11
| ||
| 70 |
∴θ=arccos
11
| ||
| 70 |
点评：本题考查圆柱的体积公式以及异面直线所成角的求法，注意求异面直线所成角的步骤：作角，证角，求角，尤其是第二步证角不可少，易疏漏，做题时要留心，注意解题步骤的完整性．
练习册系列答案
相关题目
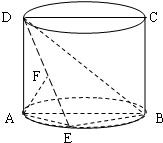如图，圆柱的轴截面ABCD是正方形，点E在底面圆周上，点F在DE上，且AF⊥DE，若圆柱的侧面积与△ABE的面积之比等于4π． 
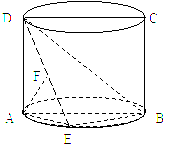如图，圆柱的轴截面ABCD是正方形，点E在底面圆周上，点F在DE上，且AF⊥DE，若圆柱的侧面积与△ABE的面积之比等于4π.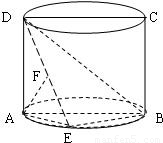
如图，圆柱的轴截面ABCD是正方形，点E在底面圆周上，点F在DE上，且AF⊥DE，若圆柱的侧面积与△ABE的面积之比等于4π. 007