题目内容
已知函数f(x)=x2-4,设曲线y=f(x)在点(xn,f(xn))处的切线与x轴的交点为(xn+1,0)(n![]()
![]() ),其中
),其中![]() 为正实数.
为正实数.
(Ⅰ)用![]() 表示xn+1;
表示xn+1;
(Ⅱ)若a1=4,记an=lg![]() ,证明数列{
,证明数列{![]() }成等比数列,并求数列{xn}的通项公式;
}成等比数列,并求数列{xn}的通项公式;
(Ⅲ)若x1=4,bn=xn-2,Tn是数列{bn}的前n项和,证明Tn<3.
(1)![]() (2)见解析(3)见解析
(2)见解析(3)见解析
解析:
(Ⅰ)由题可得![]() .
.
所以曲线![]() 在点
在点![]() 处的切线方程是:
处的切线方程是:![]() .
.
即![]() .令
.令![]() ,得
,得![]() .
.
即![]() .显然
.显然![]() ,∴
,∴![]() .
.
(Ⅱ)由![]() ,知
,知![]() ,同理
,同理![]() .
.
故![]() .从而
.从而![]() ,即
,即![]() .
.
所以,数列![]() 成等比数列.
成等比数列.
故![]() .即
.即![]() .从而
.从而![]() 所以
所以![]()
(Ⅲ)证明:由(Ⅱ)知![]() ,∴
,∴![]()
∴![]() 当
当![]() 时,显然
时,显然![]() .
.
当![]() 时,
时,![]()
∴![]()
![]()
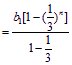
![]() .
.
综上,![]()
![]() .
.

练习册系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|