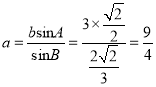题目内容
【题目】抛物线
（
）的焦点为
，已知点
， 
为抛物线上的两个动点，且满足
.过弦
的中点
作抛物线准线的垂线
，垂足为
，则
的最大值为__________．
【答案】1
【解析】设
，在三角形ABF中，用余弦定理得到
， 
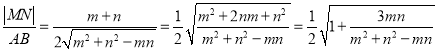
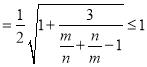故最大值为1.
故答案为：1.
点睛：本题主要考查了抛物线的简单性质．解题的关键是利用了抛物线的定义。一般和抛物线有关的小题，很多时可以应用结论来处理的；平时练习时应多注意抛物线的结论的总结和应用。尤其和焦半径联系的题目，一般都和定义有关，实现点点距和点线距的转化。
【题型】填空题
【结束】
17
【题目】设
的内角
， 
， 
所对的边分别为
， 
， 
，且
， 
.
（1）当
时，求
的值；
（2）当
的面积为
时，求
的周长.
【答案】(1) 
(2)8
【解析】试题分析：（1）由
， 
，由正弦定理得到
；（2）根据面积公式得到
，再由余弦定理得到
，进而得到
.
解析：
（1）因为
，所以
由正弦定理
，可得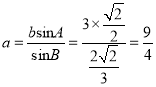
（2）因为
的面积
所以
由余弦定理
得
，即
所以
，
所以
所以， 
的周长为
练习册系列答案
相关题目
