题目内容
【题目】已知数列
的前
项和为
，并且满足
， 
.
（1）求数列
通项公式；
（2）设
为数列
的前
项和，求证： 
.
【答案】(1) 
(2)见解析
【解析】试题分析：（1）根据题意得到
， 
，两式做差得到
；（2）根据第一问得到
，由错位相减法得到前n项和，进而可证和小于1.
解析：
（1）∵
当
时， 
当
时， 
，即
∴数列
时以
为首项， 
为公差的等差数列.
∴
.
（2）∵
∴
①
②
由①
②得
∴
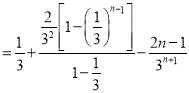
点睛：这个题目考查的是数列通项公式的求法及数列求和的常用方法；数列通项的求法中有常见的已知
和
的关系，求
表达式，一般是写出
做差得通项，但是这种方法需要检验n=1时通项公式是否适用；数列求和常用法有：错位相减，裂项求和，分组求和等.
【题型】解答题
【结束】
22
【题目】已知
， 
分别是椭圆
： 
（
）的左、右焦点， 
是椭圆
上的一点，且
，椭圆
的离心率为
.
（1）求椭圆
的标准方程；
（2）若直线
： 
与椭圆
交于不同两点
， 
，椭圆
上存在点
，使得以
， 
为邻边的四边形
为平行四边形（
为坐标原点）.
（ⅰ）求实数
与
的关系；
（ⅱ）证明：四边形
的面积为定值.
【答案】(1) 
(2)①
② 四边形
的面积为定值，且定值为
【解析】试题分析：（1）根据题意得到
， 
，椭圆的标准方程为
；（2）联立直线和椭圆方程得到二次方程，根据题意得到
，由韦达定理得到P点坐标，再根据点在椭圆上得到参数值关系；（3）先由弦长公式得到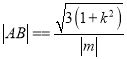
，由点线距得到三角形高度，再根据四边形面积公式
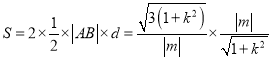，进而得到定值.
解析：
（1）依题意， 
，即
.
又
，∴
∴
故椭圆的标准方程为
（2）（ⅰ）由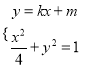
消
得
.
则
设
， 
，则
， 
.
∴
∵四边形
为平行四边形.
∴
∴点
坐标为
∵点
在椭圆
上，
∴
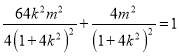，整理得
（ⅱ）∵
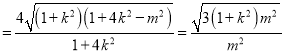
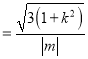
又点
到直线
： 
的距离为
∴四边形
的面积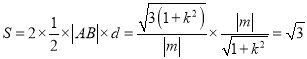
故四边形
的面积为定值，且定值为
.
