Question

如图，四棱锥S-ABCD的底面为正方形，SD⊥平面ABCD，SD=AD=3，E为线段SD上的一点．
（1）求证：AC⊥BE；
（2）若DE=1，求直线SC与平面ACE所成角的正弦值．

Answer 1

（本题满分10分）
解 （1）因为四棱锥S-ABCD的底面为正方形，SD⊥平面ABCD，
所以SD，DC，DA两两互相垂直，建立如图所示的空间直角坐标系
D-xyz，则各点的坐标为D（0，0，0），A（3，0，0），
B（3，3，0），C（0，3，0），S（0，0，3），…（2分）
设E（0，0，t） （0≤t≤3），则
=（-3，3，0），=（-3，-3，t）．
所以=-3×（-3）+3×（-3）+0×t=0，
所以，即AC⊥BE； …（5分）
（2）因为DE=1，所以t=1，所以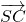=（0，3，-3），=（-3，3，0），=（-3，0，1）．
设平面ACE的法向量=（x，y，z），直线SC与平面ACE所成角为θ，
所以•=0，•=0，即-3x+3y=0，-3x+z=0，解得x=y，z=3x．
取x=1，则=（1，1，3），…（8分）
所以•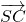=0×1+3×1+（-3）×3=-6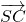，||=，||=3，
则sinθ=|cos＜，＞|=||==．
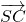所以直线SC与平面ACE所成角的正弦值为． …（10分）
说明：第（1）问：建系设坐标给（2分），若没有指出SD，DC，DA两两互相垂直，不扣分；写对，的坐标各给（1分）；
第（2）问：分两步给分，求出法向量给（3分），求出角的正弦给（2分），若把它当成余弦扣（1分）．
分析：（1）SD，DC，DA两两互相垂直，建立空间直角坐标系，求出ABCS点的坐标，设出E的坐标，求出向量，通过向量的数量积证明AC⊥BE；
（2）通过DE=1，求出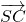，设出平面ACE的法向量，通过•=0，•=0，求出，然后利用公式求出直线SC与平面ACE所成角的正弦值．
点评：本题考查直线与直线的垂直的判断，直线与平面所成角的大小的求法，本题的解题的关键是空间直角坐标系的建立，以及公式的灵活应用，考查计算能力，空间想象能力．