题目内容
已知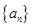 为等差数列,且
为等差数列,且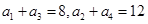 .
.
(1)求数列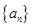 的通项公式;
的通项公式;
(2)记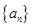 的前
的前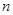 项和为
项和为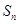 ,若
,若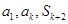 成等比数列,求正整数
成等比数列,求正整数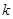 的值.
的值.
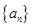 为等差数列,且
为等差数列,且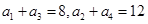 .
.(1)求数列
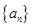 的通项公式;
的通项公式;(2)记
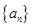 的前
的前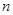 项和为
项和为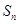 ,若
,若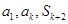 成等比数列,求正整数
成等比数列,求正整数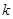 的值.
的值.(1) ;(2)
;(2) .
.
 ;(2)
;(2) .
.试题分析:(1)设公差为
 ,依题意列出关于
,依题意列出关于 的方程组
的方程组 ,从中求解即可得到
,从中求解即可得到 的取值,从而代入
的取值,从而代入 可得到数列
可得到数列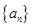 的通项公式;(2)由(1)先求出公式
的通项公式;(2)由(1)先求出公式 求出
求出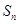 ,进而列出等式
,进而列出等式 ,然后转化为关于
,然后转化为关于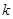 的方程,进行求解即可.
的方程,进行求解即可.试题解析:(1)设数列
 的公差为
的公差为 ,由题意知
,由题意知 解得
解得
所以

(2)由(1)可得
 因
因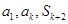 成等比数列,所以
成等比数列,所以 从而
从而 ,即
,即
解得
 或
或 (舍去),因此
(舍去),因此 .
.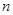 项和;2.等比数列的定义.
项和;2.等比数列的定义.
练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案
相关题目
 是各项均不为零的
是各项均不为零的 (
( )项等差数列,且公差
)项等差数列,且公差 .
. ,且该数列前
,且该数列前 最大,求
最大,求 ,且将此数列删去某一项后得到的数列(按原来的顺序)是等比数列,求
,且将此数列删去某一项后得到的数列(按原来的顺序)是等比数列,求 的值;
的值; ,则数列
,则数列 中,
中, ,
, (
( 是常数,
是常数, ),且
),且 成公比不为
成公比不为 的等比数列.
的等比数列. 满足
满足 ,则
,则 项和为
项和为  中的最大项是第
中的最大项是第 项,则
项,则 ( )
( ) 中,已知
中,已知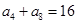 ,则该数列前11项和
,则该数列前11项和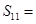 ( )
( )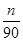 (21n-n2-5)(n=1,2,…,12),按此预测,在本年度内,需求量超过1.5万件的月份是________.
(21n-n2-5)(n=1,2,…,12),按此预测,在本年度内,需求量超过1.5万件的月份是________. 的前
的前 项和为
项和为 ,则
,则
 中,
中, ,
, ,
, ,则
,则
 = .
= .