题目内容
已知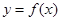 的定义域为
的定义域为 ,且恒有等式
,且恒有等式 对任意的实
对任意的实
数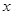 成立.
成立.
(Ⅰ)试求 的解析式;
的解析式;
(Ⅱ)讨论 在
在 上的单调性,并用单调性定义予以证明.
上的单调性,并用单调性定义予以证明.
【答案】
(Ⅰ)f(x)=[2^(-x)-2^(x+1)]/3
(Ⅱ)函数在R上为减函数,证明见解析。
【解析】本试题主要是考查了求解函数的解析式,以及函数单调性的证明。
(1)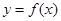 的定义域为
的定义域为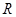 ,且恒有等式
,且恒有等式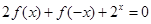 对任意的实数
对任意的实数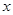 成立.,那么可以得到方程组,消元法得到结论。
成立.,那么可以得到方程组,消元法得到结论。
(2)设出变量,运用定义法证明单调性。
解:
1、2f(x)+f(-x)+2^x=0 …………1
2f(-x)+f(x)+2^(-x)=0 …………2
1式X2-2式得:
3f(x)+2^(x+1)-2^(-x)=0
即:f(x)=[2^(-x)-2^(x+1)]/3
2、设x1<x2 可得:
f(x1)-f(x2)
=[2^(-x1)-2^(x1+1)]/3-[2^(-x2)-2^(x2+1)]/3
=[2^(-x1)-2^(-x2)]/3+[2^(x2+1)-2^(x1+1)]/3
因:x1<x2 所以有:-x1>-x2 ,x1+1<x2+1
所以:2^(-x1)>2^(-x2)
2^(x2+1)>2^(x1+1)
即:f(x1)-f(x2)>0
所以此函数在R上为减函数!

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
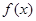 定义域为
定义域为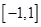 ,若对于任意的
,若对于任意的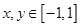 ,都有
,都有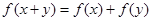 ,且
,且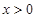 时,有
时,有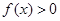 .
.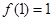 ,若
,若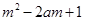 ,对所有
,对所有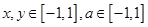 恒成立,求实数
恒成立,求实数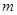 的取值范围.
的取值范围.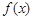 的定义域为
的定义域为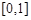 ,且同时满足:①
,且同时满足:①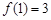 ;②
;②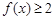 恒成立;③若
恒成立;③若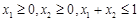 ,则有
,则有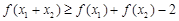 .
. 与
与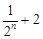 的大小
的大小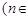 N);
N); (nÎN)时,有f(x)<2x+2.由此他提出猜想:对一切xÎ(0,1
(nÎN)时,有f(x)<2x+2.由此他提出猜想:对一切xÎ(0,1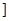 ,都有
,都有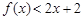 ,请你判断此猜想是否正确,并说明理由.
,请你判断此猜想是否正确,并说明理由.